Учебное пособие по курсу "Теория механизмов и машин", страница 23

 = /l_CD = 0,103²/0,1 = 0,106 м/с².

 Из трех известных векторов наибольшим является . Масштаб плана ускорений:

                     m_a = pn₂/ = 53/0,106 = 500 мм/(м×с^-2).                   

Длины векторов:

       pk = m_a = 0,033×500 = 17 мм; kn₁ = 0,0042×500 = 2 мм.     

Из полюса p (рис. 4.5, г) проводим вектор pk = 17 мм перпендикулярно AC в сторону w₁. Из его конца проводим вектор kn₁ параллельно AC и направление , ему перпендикулярное. Решая второе уравнение системы, из полюса p проводим вектор pn₂ = 53 мм. Из его конца проводим направление . Пересечение направлений тангенциальных составляющих даст искомую точку c. Длины отрезков:

                        n₁c = 74 мм; n₂c = 17 мм; pc = 57 мм.                      

Величины ускорений:

                       a_C = a_CD = pc/m_a = 57/500 = 0,114 м/с²;                     

                           = n₁c/m_a = 74/500 = 0,148 м/с²;                       

                          = n₂c/m_a = 17/500 = 0,034 м/с².                       

Угловые ускорения:

                          e₁ = /l_AC = 0,148/0,16 = 0,91 c^-2;                       

                         e₃ = /l_CD = 0,034/0,1 = –0,34 c^-2.                       

Направления угловых ускорений определяем после приложения тангенциальных составляющих в точку C плана положений (рис. 4.5, б). Направление e₁ — положительное, e₃ — отрицательное.

4.4. Метод кинематических диаграмм

Кинематическое исследование механизмов необходимо бывает проводить за полный цикл движения. При этом аналитическое или графическое исследование перемещений, скоростей и ускорений ведут для ряда положений механизма, достаточно близко отстоящих друг от друга. Полученные величины кинематических параметров сводят в таблицы либо строят графики, носящие название кинематических диаграмм. В практических задачах ТММ кинематическая диаграмма обычно представляет собой графическое изображение изменения одного из кинематических параметров: перемещения, скорости или ускорения в функции времени или перемещения начального звена механизма, т.е. в функции обобщенной координаты.

Например, в кривошипно-ползунном механизме (рис. 4.2, а) для перемещений s_C, скоростей u_C и ускорений a_C точки С, движущейся прямолинейно, удобно строить кинематические диаграммы в виде зависимостей этих величин от обобщенной координаты j либо от времени t, т.е. строить графическое изображение зависимостей

                                             или

                     .                  

В других случаях требуется построение и других зависимостей, например, . Диаграмму перемещений точки С ползуна строят по планам положений механизма, например, по 12-ти планам (рис. 4.2, а), для одного оборота кривошипа в масштабе m_s = nm_l, где n — коэффициент пропорциональности. Отсчет перемещений точки С удобно вести от крайнего левого положения ползуна 9 (нижней мертвой точки, НМТ). Проводят две оси координат (рис. 4.2, б) и на оси абсцисс откладывают отрезок , изображающий в масштабе  время Т одного полного оборота кривошипа. Масштаб времени, мм/с:

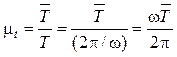                                  .                        (4.34)

В точках 8, 7, 6 и т.д. деления отрезка откладывают расстояния, пройденные точкой С от НМТ ползуна. Так, например, в точке 8 откладывают в масштабе  в направлении оси ординат отрезок 9–8, в точке 7 — отрезок 9–7 и т.д. Если отрезки откладывать прямо с плана положений механизма, то  и n = 1. Полученная плавная кривая (рис. 4.2, б) является диаграммой перемещений точки С от НМТ ползуна.

Так как кривошип вращается с постоянной угловой скоростью , то можно считать, что по оси абсцисс отложено не только время t, но и углы поворота  звена АВ, т.е. диаграмма  будет одновременно и диаграммой . Масштаб угла поворота, мм/рад (мм):

                                                                (4.35)

Для построения диаграмм  и  отрезки, изображающие на планах скоростей и ускорений  и a_C, полученные графическим методом или рассчитанные аналитически, откладывают на ординатах, проведенных в точках 9, 8, 7, 6 и т.д. с учетом знаков скоростей и ускорений.