Учебное пособие по курсу "Теория механизмов и машин", страница 89

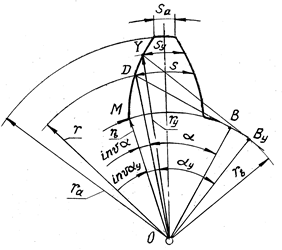
Рис. 14.19

Из точек эвольвенты D и Y, соответствующих делительной и произвольной окружностям, проводят нормали, которые касаются основной окружности в точках B и B_y. Проведенные в эти точки из центра колеса O перпендикуляры располагаются по отношению к текущим радиусам-векторам под углами соответственно a и a_y. Текущие радиусы-векторы составляют с начальным радиусом-вектором ОМ углы inva и inva_y. Из ОDB находят основной радиус:

r_b = r cosa = 0,5mz cosa.                               

Аналогично основной диаметр

                                           d_b = d cosa.                               (14.30)

С учетом формулы (14.30) передаточное отношение может быть рассчитано не только по начальным, но и по основным диаметрам:

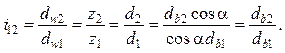                                    (14.31)

Поскольку основные диаметры не меняются при смещении инструмента, передаточное отношение в эвольвентном зацеплении постоянно.

NB 14.16. Передаточное отношение в эвольвентном зацеплении постоянно, так как определяется отношением основных диаметров, остающихся неизменными при любых смещениях.

Рассмотренные положения характеризуют одно из основных свойств эвольвентного зубчатого зацепления — свойство постоянства передаточного отношения. Другое важное свойство — свойство нечувствительности передаточного отношения к ошибкам сборки.

На рис. 14.17 изображены две передачи: точной сборки (рис. 14.17, а) и неточной сборки (рис. 14.17, б) с увеличенным на a межосевым расстоянием. Для точной сборки передаточное отношение

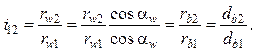                                          (14.32)

При неточной сборке

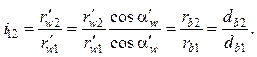                                         (14.33)

Из формул (14.32) и (14.33) следует, что при сборке любой точности передаточное отношение эвольвентной зубчатой передачи остается постоянным.

NB 14.17. Эвольвентная зубчатая передача нечувствительна к изменению межосевого расстояния, так как передаточное отношение определяется отношением основных диаметров.

14.12.2. Углы профиля

Для эвольвенты радиуса-вектора произвольной окружности r_у определяют из ОDB_y (см. рис. 14.19):

                                          r_у = r_b/cos a_у.                              (14.34)

Из формул (14.30) и (14.32) следует:

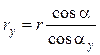                                          ,                              (14.35)

откуда угол профиля по произвольной окружности

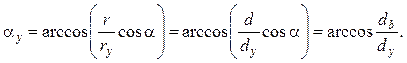           (14.36)

Отсюда следует, что угол профиля зависит от радиуса окружности, по которой он определяется. В частности, по делительной окружности, когда d_y = d, угол профиля a = 20°; угол профиля по начальным окружностям равен углу зацепления . Наибольший угол профиля — по окружности вершин. Вследствие ограничения диаметра вершин по условию незаострения (рассматривается в п. 14.13) максимальный угол профиля  не превышает 60°.

NB 14.18. С увеличением радиуса окружности угол профиля увеличивается.

Так как шаги пропорциональны радиусам, то основной шаг в соответствии с формулой (14.30):

p_b = p cosa = pm cosa.                       (14.37)

Шаг по окружности произвольного радиуса определяют аналогично формуле (14.35):

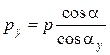                                         .                             (14.38)

14.12.3. Толщины зубьев

Как известно, длина дуги окружности определяется произведением радиуса на угол. Длина дуги произвольной окружности r_y (см. рис. 14.19):

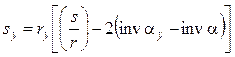                            .                (14.39)

В формуле (14.39) в квадратных скобках — угол сектора толщины зуба по произвольной окружности, определяемый как разность угла сектора делительной толщины зуба и удвоенной разницы эвольвентных углов по окружностям — произвольной и делительной. С учетом зависимости (14.28) после замены радиусов диаметрами получают:

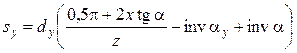                      .          (14.40)

В частности, для проверки отсутствия заострения по вершинам зубьев шестерни рассчитывают s_a по формуле (14.40), в которой вместо d_y и a_y ставят d_a и a_a. Угол a_a рассчитывают по формуле (14.36). В результате

                                     ;                                   

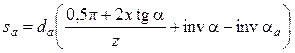                       .         (14.41)