Машиностроение \ Теории механизмов и машин

Учебное пособие по курсу "Теория механизмов и машин", страница 10

Присоединение к начальному механизму I класса диады 4-го вида образует тангенсный механизм (рис. 3.15), где звено 1 — кулиса, 2 — камень кулисы, 3 — ползун. Заметим, что в тангенсном механизме отсутствует кривошип. Присоединение диады 5-го вида образует синусный механизм (рис. 3.16). Здесь звено 1 — кривошип, 2 — камень кулисы, 3 — кулиса.

Рис. 3.15

Рис. 3.16

3.8. Структурный анализ плоских рычажных механизмов

NВ 3.8. Структурный анализ заключается в отсоединении групп Ассура по заданной схеме механизма.

NB 3.9. Порядок структурного анализа:

1)  рассчитывают число степеней свободы по формуле Чебышева;

2)  начинают отсоединение с групп Ассура, наиболее удаленных от начального звена;

3)  отсоединяют в первую очередь двухповодковые группы (диады) с n = 2 и p1 = 3, чтобы не принять несколько простых групп за одну группу более высокого класса;

4)  после отсоединения групп Ассура должны остаться начальные механизмы I класса, число которых равно числу степеней свободы механизма.

Пример 3.3. Выполнить структурный анализ восьмизвенного механизма (рис. 3.17).

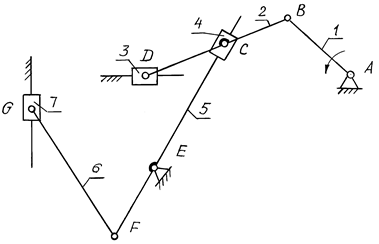
Рис. 3.17

Решение:

Вычерчиваем кинематическую схему. Составляем таблицу звеньев и пар (табл. 3.5).

Таблица 3.5

Обозначение

кинематических пар

Номера звеньев, входящих в пару

Вид пары (вращательная, поступательная)

A

0–1

Вращательная

B

1–2

Вращательная

C

2–4

Вращательная

C

4–5

Поступательная

D

2–3

Вращательная

D

3–0

Поступательная

E

5–0

Вращательная

F

5–6

Вращательная

G

6–7

Вращательная

G

7–0

Поступательная

Число подвижных звеньев механизма n = 7, число низших пар p1 = 10. Число степеней механизма W = 3×7 – 2×10 = 1. Отсоединяем наиболее удаленную диаду 2-го вида, состоящую из звеньев 6 и 7, затем диаду 3-го вида (звенья 4 и 5) и, наконец, диаду 2-го вида (2 и 3). Остается один начальный механизм I класса, так как W = 1 (рис. 3.18).

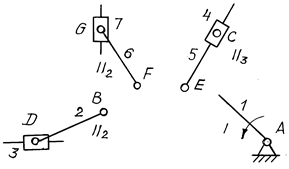
Рис. 3.18

На основании структурного анализа выводят формулу строения механизма. Вначале ставят римскую цифру I, символизирующую начальный механизм I класса. Ее связывают линией с римской цифрой, обозначающей класс ближайшей группы Ассура, следующая линия — связывает с цифрой, обозначающей класс следующей группы Ассура и т.д. В диадах в индексе ставится вид, в группах Ассура III и более высокого класса в индексе ставится порядок группы.

NB 3.10. Класс механизма определяют по той группе Ассура, которая относится к наивысшему классу.

В примере 3.3 формула строения механизма:

                          I(1) – II2(2, 3) – II3(4, 5) – II2(6, 7).                        

В формуле строения в скобках указаны номера звеньев. Данный восьмизвенный механизм относится ко II классу, так как в его состав входят только группы Ассура II класса.

3.9. Замена высших пар низшими

В состав плоских механизмов могут входить двухподвижные (высшие) кинематические пары. При структурном анализе механизмов их предварительно заменяют эквивалентными заменяющими механизмами с низшими парами.

Замена будет правомерной при условии структурной и кинематической эквивалентности. Первое условие предполагает равенство чисел степеней свободы заданного и заменяющего механизмов. Оба условия будут выполнены при соблюдении следующего правила:

NВ 3.11. Высшую кинематическую пару заменяют кинематической цепью, состоящей из одного звена и двух низших пар.

Рис. 3.19

Чтобы заменить высшую пару низшей, через точку касания профилей проводят нормаль к соприкасающимся профилям (рис. 3.19). В центрах кривизны, находящихся на нормалях, ставят две вращательные кинематические пары и соединяют их дополнительным звеном друг с другом и с кинематическими парами ближайших звеньев. В заданном трехзвенном механизме W = 3×2 – 2×2 – 1 = 1, в заменяющем механизме также W = 3×3 – 2×4 = 1.

Скачать файл