Учебное пособие по курсу "Теория механизмов и машин", страница 31

При равномерном вращении (e₁ = 0) угловое ускорение шатуна

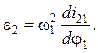                                                                          (5.52)

С учетом формулы (5.50) аналог углового ускорения:

           =  =         

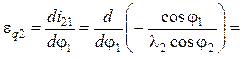
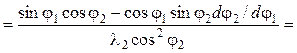
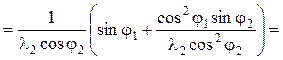
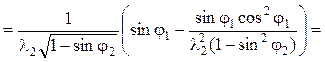
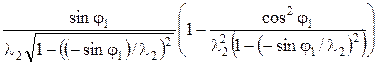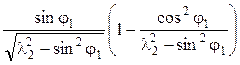                          = ,                (5.53)

откуда угловое ускорение шатуна:

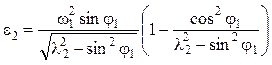.            (5.54)

Из формулы (5.46) координата точки С ползуна 3:

                               .                     (5.55)

Аналог скорости точки С ползуна

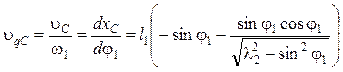                 ,       (5.56)

откуда скорость точки С ползуна

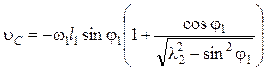                         .               (5.57)

Повторное дифференцирование дает ускорение

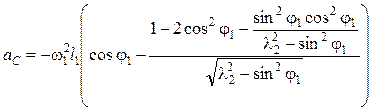              .   (5.58)

Функции положения точки S₂ на шатуне 2, проекции скоростей и ускорений точки S₂, полные скорости и ускорения _S2 и a_S2, а также их угловые расположения рассчитывают по формулам (5.37) – (5.43). Линейную скорость _В рассчитывают по формуле (4.11), линейное ускорение а_В — по формуле (4.20).

Пример 5.2. Рассчитать по программе ТМM-1 кинематические параметры кривошипно-ползунного механизма для 12 положений кривошипа по исходным данным примера 4.1: длины звеньев: l₁ = = 0,08 м; l_BС = 0,3 м, l_BS2 = 0,09 м; угловая скорость w₁ = 215 с^-1, угловая координата кривошипа  = 0 – 360° с шагом  = 30°.

Решение:

Выполняем расчеты по программе ТМM-1 в системе Quick BASIC. Распечатка компьютерных данных приведена на рис. 4.8. Данные для сравнения графических (примеры 4.1 и 4.2) и аналитических методов для положения 2 кривошипа приведены в табл. 5.5.

Таблица 5.5

Вывод:

Отклонения находятся в допустимых пределах.

5.5. Аналитические зависимости кинематических параметров кривошипно-кулисного механизма

Из векторного контура АВС (рис. 5.8) записывают векторное равенство:

                                            .                                 (5.59)

Уравнения проекций на оси координат:

                                      ;                            (5.60)

                                   .                         (5.61)

Переменную величину l₃ находят по теореме косинусов:

                                 .                      (5.62)

После деления уравнения (5.61) на (5.60) получают:

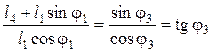                              ,                             откуда

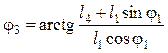                                   .                        (5.63)

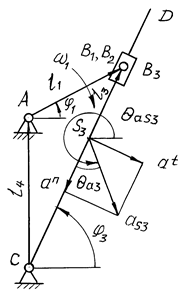
Рис. 5.8

Для определения скоростей кулисы уравнения (5.60) и (5.61) дифференцируют по обобщенной координате φ₁:

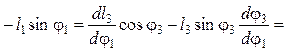
                               ;                    (5.64)

                         ,              (5.65)

где υ_qB3B2 — аналог относительной скорости υ_B3B2; i₃₁ = ω₃/ω₁ — аналог угловой скорости кулисы.

Из углов уравнений (5.64) и (5.65) вычитают угол φ₃:

                         ;              (5.66)

                                    .                         (5.67)

Из уравнения (5.66) определяют относительную скорость:

                                 υ_B3B2 = –ω₁l₁sin (φ₁ – φ₃).                      (5.68)

Из уравнения (5.67) находят угловую скорость кулисы:

                                l₁ cos (φ₁ – φ₃) = (ω₃/ω₁) l₃;                              

                                 ω₃ = ω₁ l₁ cos (φ₁ – φ₃)/l₃.                      (5.69)