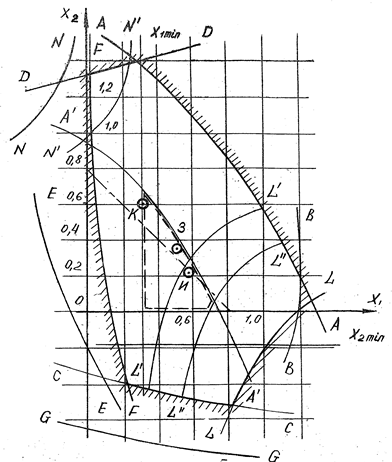
Рис. 14.25
С учетом ограничений по дополнительным условиям синтеза рекомендуемая область значительно меньше основного контура. Она ограничена линиями х1 min = 0,3; х2 = 0; ea = 1,2; sa1 = 0,25m и показана на рис. 14.25 штриховыми линиями.
Пример 14.4. Коэффициент суммы смещений зубчатой передачи 12/20 хS = 0,8. Выбрать по блокирующему контуру коэффициенты смещения из условий:
а) контактной прочности;
б) изгибной прочности.
Решение:
На обеих координатных осях х1 и х2 блокирующего контура (см. рис. 14.25) откладываем хS = 0,8 и полученные точки соединяем штрихпунктирной прямой. На этой прямой в пределах контура можно выбрать любую точку. Опустив из нее перпендикуляры на координатные оси, получаем искомые коэффициенты смещения; при этом следует знать, что а) при неизменном коэффициенте суммы смещений хS контактная прочность не меняется;
б) смещение наиболее эффективно для шестерни, имеющей более низкую изгибную прочность, чем колесо; принимаем х1 = 0,6; х2 = хS – х1 = 0,8 – 0,6 = 0,2.
На блокирующий контур 12/20 также нанесены точки К, И и З, соответствующие табличным значениям. Табличные коэффициенты смещения по максимальной изгибной прочности (х1 = 0,57; х2 = 0,25, см. табл. 14.3) практически совпадают с выбранными нами из контура.
Делительное межосевое расстояние а может не соответствовать стандартному либо заданному значению aw. Расчет коэффициентов смещения, удовлетворяющих цели вписывания в межосевое расстояние, ведут в следующей последовательности:
1) рассчитывают коэффициент воспринимаемого смещения (см. пример 14.3);
2) угол зацепления — из формулы (14.50);
3) коэффициент суммы смещений — из формулы (14.44):
; (14.59)
4) коэффициент уравнительного смещения (см. пример 14.3);
5) разбивку коэффициента суммы смещений на х1 и х2 выполняют либо по блокирующему контуру, либо по таблицам.
Пример 14.5.
По данным примера 13.1 при модуле m = 6 мм выбрать коэффициенты смещения, обеспечивающие одинаковые межосевые расстояния (соосность) зацеплений z1/z2
и 
редуктора Давида (см. рис. 13.2).
Числа зубьев: z1 = 100, z2 = 99, 
= 100, z3 = 101.
Решение:
1. Делительные межосевые расстояния:
a12 = 0,5m (z1 + z2) = 0,5×6 (100 + 99) = 597 мм,
a23 = 0,5m (100 + 101) = 603 мм.
2. Принимаем межосевые расстояния обоих зацеплений: аw12 = = аw23 = а23 = 603 мм.
3. Коэффициенты смещения зацепления ; принимаем: 
= 0, х3 = 0.
4. Для зацепления z1/z2 коэффициент воспринимаемого смещения
.
5. Угол зацепления
.
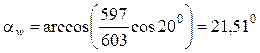6. Коэффициент суммы смещений
хS = (inv21,510 – inv200)×(100 + 99)/(2tg200) = 1,045.
7. Коэффициент уравнительного смещения
Dy = 1,045 – 1 = 0,045.
8. Для зацепления 100/99 рекомендации по выбору табличных коэффициентов смещения и блокирующие контуры отсутствуют. Принимаем примерно равные их значения: х1 = 0,5; х2 = 0,545.
9. Делительные диаметры колес:
d1 = 6 ×100 = 600 мм, d2 = 6 × 99 = 594 мм.
10. Начальные диаметры
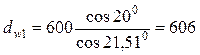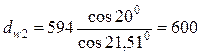мм; 
мм.
Проверка:
aw12 = 0,5 (dw1 + dw2) = 0,5 (606 + 600) = 603 мм.
Вывод:
Рассчитанные коэффициенты смещения обеспечивают соосность обоих зацеплений.
К качественным показателям зацепления относятся:
– коэффициент перекрытия — см. п. 14.13.4;
– удельное скольжение;
– коэффициент давления;
– коэффициент формы зуба.
Удельное скольжение учитывает влияние геометрических и кинематических факторов на величину проскальзывания профилей в процессе зацепления. Наличие скольжения в сочетании с контактными напряжениями приводит к износу профилей зубьев.
Удельное
скольжение равно отношению скорости скольжения профилей 
s к тангенциальной
составляющей скорости точки контакта t
(см. п. 14.3). Удельные скольжения шестерни и колеса:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.