Учебное пособие по курсу "Теория механизмов и машин", страница 19

Пример 4.3. Выполнить структурный и кинематический анализ кривошипно-коромыслового механизма (рис. 4.3, а) по следующим исходным данным: угловая скорость кривошипа w₁ = 150 с^-1, длины звеньев: l_AB = 0,1 м; l_BC = 0,2 м; l_CD = 0,3 м; l_AD = 0,35 м; координаты центров масс l_BS2 = 0,4×l_BC = 0,08 м; l_DS3 = 0,3×l_CD = 0,09 м, угловая координата кривошипа j₁ = 60°.

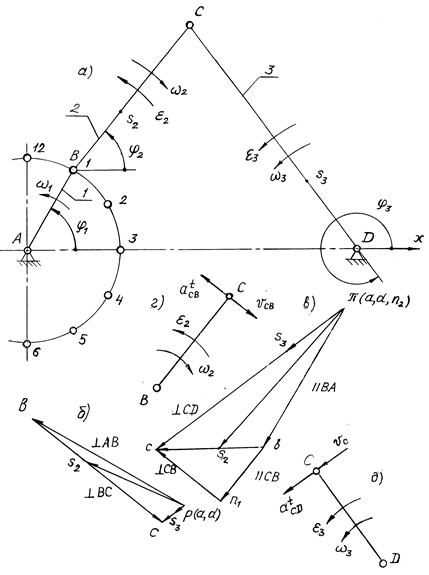
Рис. 4.3

Решение:

1. Для построения плана положений звено AB изображаем в масштабе m_l = 40/0,1 = 400 мм/м — формула (4.7). Длины отрезков на плане положений:

                 BC = 0,2×400 = 80 мм; CD = 0,3×400 = 120 мм;               

                                 AD = 0,35×400 = 140 мм;                               

               BS₂ = 0,08×400 = 32 мм; DS₃ = 0,09×400 = 36 мм.             

Длину отрезка AB = 40 мм откладываем в заданном положении кривошипа. Точку C находим методом засечек на пересечении двух дуг окружностей с радиусами BC и CD.

2. Структурный анализ. Данный механизм состоит из трех подвижных звеньев (n = 3) и четырех одноподвижных кинематических пар (p₁ = 4). Число степеней свободы по формуле Чебышева W = 3×3 – 2×4 = 1. Механизм состоит из начального механизма I класса (звено 1) и диады 1-го вида 2–3.

3. Искомая точка C. Составляем систему векторных уравнений для построения плана скоростей аналогично (4.13):

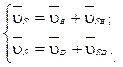                                                                      (4.29)

Скорость точки B _B = 150×0,1 = 15 м/с. Масштаб плана скоростей m_l = pb/_B = 75/15 = 5 мм/(м×с^-1) — формула (4.14). Вектор pb = 75 мм проводим перпендикулярно AB в сторону вращения. Из его конца проводим направление _CB перпендикулярно CB. Из полюса p (так как _D = 0) проводим направление _CD, перпендикулярное CD, до пересечения с направлением _CB. В искомую точку c проводим стрелки векторов. Длины векторов и значения скоростей:

                  pc = 12 мм; _C = 12/5 = 2,4 м/с; bc = 71 мм;                

_CB = 71/5 = 14,2 м/с.                                 

На отрезках bc и pc находим положения точек s₂ и s₃ из свойства подобия планов:

                                                bs₂ = 0,4bc = 0,4×71 = 28 мм;                          

                              ps₃ = 0,3pc = 0,3×12 = 3,6 мм.                           

Длины векторов и скорости центров масс:

ps₂ = 47 мм; _S2 = 47/5 = 9,4 м/с;                        

                         ps₃ = 3,6 мм; _S3 = 3,6/5 = 0,72 м/с.                       

Угловые скорости звеньев:

    w₂ = _CB/l_CB = 14,2/0,2 = –71 с^-1; w₃ = _CD/l_CD = 2,4/0,3 = 8 с^-1.  

Знаки соответствуют направлениям угловых скоростей (рис. 4.3, г, д).

4. Система векторных уравнений для построения плана ускорений аналогична (4.23):

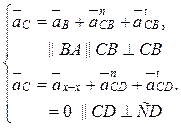
Угловое ускорение точки B (нормальная составляющая, тангенциальное ускорение отсутствует, так как e₁ = 0):

                                 a_B = 150²×0,1 = 2250 м/с².                               

Масштаб плана ускорений m_a = pb/a_B = 67,5/2250 = 0,03 мм/(м×с^-2). Вектор pb = 67,5 мм (рис. 4.3, в) проводим параллельно BA к точке вращения A. Из его конца проводим направление, параллельное . Величины нормальных составляющих относительных ускорений:

                      = 14,2²/0,2 = 1008,2 м/с²;                   

                         = 2,4²/0,3 = 19,2 м/с².                      

Длины отрезков, изображающих нормальные ускорения:

      bn₁ = m_a = 1008,2×0,03 = 30 мм; pn₂ = 19,2×0,03 = 0,6 мм.    

Вектор bn₁ = 30 мм направляем из точки b параллельно звену CB в сторону точки B (рис. 4.3, б). Из его конца проводим направление, перпендикулярное звену CB. Решая второе векторное уравнение, из полюса p (так как a_D = 0 и πn₂ ≈ 0) проводим направление, перпендикулярное CD, до пересечения с направлением . В полученную точку c направляем стрелки векторов. Длины векторов:

                       bc = 46 мм; n₁c = 36 мм; pc = 100 мм.