Для нарезания эвольвентных зубьев наибольшее распространение получил реечный инструмент, так как профиль зуба эвольвентной рейки представляет собой прямую линию. На рис. 14.6 показан контур зубьев реечного инструмента.
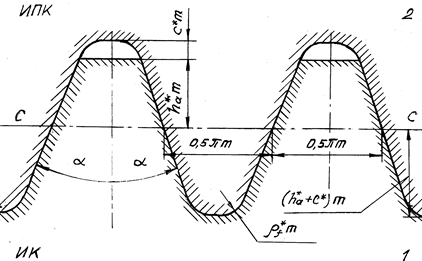
Рис. 14.6
Контур 1 называется исходным контуром (ИК), так как он определяет размеры зубчатого колеса, являясь его своеобразным шаблоном. Контур 2 называется исходным производящим контуром (ИПК), так как ему соответствуют размеры режущего инструмента. Он отличается от ИК большей высотой головки, которая формирует впадину зуба, гарантирующей постоянный стандартный радиальный зазор с.
Главной линией ИПК является делительная прямая С-С, проходящая по середине контура. Она также называется средней прямой. Для цилиндрических колес стандартом предусмотрены следующие коэффициенты:
a = 200,
—
коэффициент радиального зазора; 
— коэффициент радиуса
переходной кривой; a — угол профиля;
это угол наклона профиля исходного контура.
Приведенные параметры являются стандартными и для нарезаемого колеса.
Переходную кривую максимально возможного радиуса проектируют для снижения концентрации напряжений у основания зуба.
Каждый зуб колеса (см. рис. 14.5) очерчен двумя симметрично расположенными эвольвентными профилями. Расстояние между этими профилями, измеренное по дуге окружности, называется толщиной зуба. Толщина зуба по делительной окружности обозначается через s. Ширина впадины — e.
Для нулевого колеса
s = e = 0,5p = 0,5pm. (14.18)
Высота ножки зуба больше высоты головки на величину радиального зазора:
. (14.19)
Высота зуба
. (14.20)
Диаметр вершин колеса определяется суммой делительного диаметра и двух высот головки зуба:
. (14.21)
Диаметр впадин определяется разностью делительного диаметра и двух высот ножки зуба:
. (14.22)
Угловой шаг колеса
t = 2p/z. (14.23)
В соответствии со стандартами на термины, определения и обозначения индексы обозначений несут смысловую нагрузку. Так, индекс a относится к головке (вершине), f — к ножке (впадине), w — к начальной окружности, y — к окружности произвольного радиуса. Обозначения параметров делительных окружностей дают без индекса.
Пример 14.2.
Рассчитать параметры зубчатого колеса: d, da, df,
p, s, h, 
, если задано:
модуль m = 5 мм, число зубьев z = 48. Параметры исходного
контура: 
= 1; =
0,25.
Решение:
Делительный диаметр d = 5·48 = 240 мм.
Диаметр вершин da = 5(48 + 2) = 250 мм.
Диаметры впадин df = 5(48 – 2,5) = 227,5 мм.
Шаг зубьев p
= 
·5 = 15,71 мм.
Делительная
толщина зубьев s = 0,5··5 = 7,85 мм.
Высота зубьев h = 2,25·5 = 11,25 мм.
Угловой шаг = 2/48 = 0,1309 рад; =
360/48 = 7,5º = 7º30¢.
Инструментом для изготовления колес с внутренними зубьями является не реечный инструмент, а долбяк (инструментальное колесо), число зубьев и основные размеры которого стандартизированы. При изготовлении колес долбяком может произойти не только подрезание и заострение зубьев колес, но и срезание их у вершины. Это происходит при близких значениях чисел зубьев z1 и z2. Явление, когда одна и та же площадь теоретического чертежа занята зубьями двух колес, называется интерференцией. Такую передачу либо невозможно собрать, либо она не будет работать вследствие заклинивания, когда головка зуба колеса начнет вдавливаться в ножку зуба шестерни.
Интерференция во внутреннем зацеплении отсутствует при z1 ³ 19 и других условиях в соответствии с пп. 14.13.3.
Диаметр впадин (рис. 14.7)
df = d + 2hf = m (z + 2,5). (14.24)
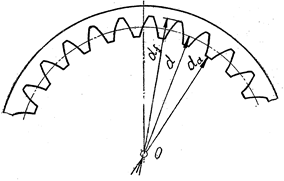
Рис. 14.7
Диаметр вершин
da = d – 2ha + (15,2/z) m = m (z – 2 + 15,2/z). (14.25)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.