|
Параметр |
Вариант |
||
|
1 |
2 |
3 |
|
|
Числа зубьев z1 |
120 |
130 |
150 |
|
z2 |
20 |
25 |
32 |
|
|
21 |
24 |
31 |
|
z3 |
119 |
131 |
151 |
|
|
22 |
24 |
26 |
|
z4 |
140 |
135 |
130 |
|
Угловая скорость w1, с-1 |
170 |
–190 |
210 |
Задача № 58 (рис. 13.18)
Рассчитать передаточное отношение каждой ступени сложного зубчатого механизма, содержащего планетарный редуктор, и общее передаточное отношение i15, общий КПД h15, если КПД одного зубчатого зацепления h = 0,96. Рассчитать угловую скорость ведомого звена w5. Вычертить кинематическую схему.
|
Параметр |
Вариант |
||
|
1 |
2 |
3 |
|
|
Числа зубьев z1 |
18 |
21 |
18 |
|
z2 |
43 |
40 |
41 |
|
|
34 |
34 |
35 |
|
z3 |
105 |
102 |
99 |
|
z4 |
96 |
96 |
93 |
|
|
18 |
21 |
18 |
|
z5 |
75 |
80 |
92 |
|
Угловая скорость w1, с-1 |
–280 |
240 |
–180 |
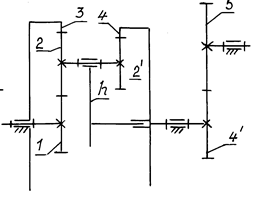
Рис. 13.18
Одноступенчатая зубчатая передача с неподвижными осями представляет собой трехзвенный механизм с одной высшей кинематической парой. Зубчатые механизмы получили очень широкое применение как в машиностроении, так и приборостроении благодаря большой надежности и точности в воспроизведении заданного закона движения. Цилиндрическая зубчатая передача является плоским механизмом. В процессе работы осуществляется перекатывание профилей зубьев, а также их проскальзывание.
Высшая кинематическая пара качения и скольжения, образуемая поверхностями зубьев, называется зубчатым зацеплением.
Профили зубчатых колес должны соответствовать друг другу, т.е. быть сопряженными.
Взаимодействующие поверхности звеньев высшей пары, обеспечивающие заданное условие их относительного движения, называются сопряженными поверхностями.
Проектирование зубчатых механизмов, выполняемое в соответствии с теорией зубчатого зацепления, содержит следующие этапы:
1. Нахождение профилей зубьев, удовлетворяющих основному условию зацепления:
![]() (14.1)
(14.1)
2. Расчет геометрических параметров зубчатых колес.
3. Расчет геометрии зубчатого зацепления.
4. Проверка дополнительных условий синтеза.
5. Расчет качественных показателей зацепления.
6. Расчет контрольных параметров.
Первый этап синтеза состоит в отыскании сопряженных поверхностей по заданному закону их относительного движения — формуле (14.1). Для решения этой задачи используется основная теорема зацепления — теорема Виллиса. Пусть передача вращения между двумя осями О1 и О2 с постоянными угловыми скоростями w1 и w2 осуществляется посредством двух звеньев — 1 и 2 с сопряженными криволинейными поверхностями (рис. 14.1, а). Проводят в точке соприкосновения С касательную t–t и нормаль n–n к этим кривым. Нормаль n–n пересечет межосевую линию О1О2 в точке W. Ее принято называть полюсом зацепления.
Скорости точек С1 и С2, принадлежащих звеньям 1 и 2, связаны условием из теоремы о сложении скоростей:
![]() . (14.2)
. (14.2)
Векторы ![]() и
и ![]() направлены
перпендикулярно радиусам О2С2 и О1С1
в сторону вращения.
направлены
перпендикулярно радиусам О2С2 и О1С1
в сторону вращения.
Строят план скоростей без учета масштаба (рис. 14,1, б). Из полюса плана р перпендикулярно О1С1 в сторону w1 проводят вектор pс1 произвольной длины. Из его конца проводят направление, параллельное t–t, соответствующее относительной скорости υС2С1; из полюса р проводят направление, перпендикулярное О2С2. В точке пересечения ставят искомую точку с2. Стрелки искомых векторов направляют по уравнению (14.2), т.е. в искомую точку с2.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.