Учебное пособие по курсу "Теория механизмов и машин", страница 43

Большинство машин работают длительное время t_у в установившемся режиме, когда скорость меняется циклически либо остается постоянной. Диаграмма  на рис. 7.1, изображающая зависимость скорости от времени, называется тахограммой. Общее время работы механизма

В большинстве машин время разбега  и выбега  — непроизводительное время. Время разбега зависит от типа машины и может составлять доли секунды (электродвигатель), десятки секунд (дизель тепловоза), часы (паровоз). Время выбега уменьшают тормозными устройствами.

7.2. Уравнения движения в энергетической форме

Одну из простых форм уравнения движения получают на основании теоремы об изменении кинетической энергии, которая для плоского механизма имеет вид:

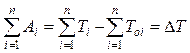                                 ,                        (7.1)

где  — кинетическая энергия звена  в конце рассматриваемого промежутка времени, Дж; для звена коромыслового типа

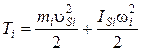                                     ,                             (7.2)

 — кинетическая энергия в начале этого промежутка;  — приращение кинетической энергии.

Сумму работ можно представить как разность работ сил движущих и сопротивления. В режиме разбега уравнение (7.1) имеет вид:

                                      .                              (7.3)

В данном режиме происходит накопление кинетической энергии, так как скорость в конце промежутка времени больше, чем в начале, т.е.  и .

При установившемся режиме

                             или .                   (7.4)

Приращение кинетической энергии в этом режиме , так как через каждый цикл движения скорость  равна . При рассмотрении произвольного промежутка времени в пределах цикла используют универсальную формулу (7.1).

В режиме выбега

                               и .                      (7.5)

В этом режиме накопленная энергия расходуется на преодоление сил сопротивления, в том числе тормозных сил, а движущая сила отсутствует (А_Д = 0).

Для установившегося движения формула может быть записана так:

                    или 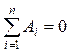,           (7.6)

где  — работа сил полезных сопротивлений;  — работа сил вредных сопротивлений;  — работа сил инерции;  — работа сил тяжести.

Продифференцировав уравнение (7.4) по времени, получают уравнение суммы мощностей:

                     или 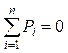.           (7.7)

Уравнения (7.6) и (7.7) называют уравнениями движения в энергетической форме или основными уравнениями динамики.

7.3. Динамическая модель машинного агрегата

Уравнения (7.6) и (7.7) представляются громоздкими даже для плоских механизмов с небольшим числом звеньев вследствие необходимости производить суммирование по n звеньям. Для механизмов с одной степенью свободы можно получить более простую запись уравнения, при которой все операции суммирования по n звеньям выполняют заранее.

С этой целью многозвенный механизм заменяют одномассовой динамической моделью, состоящей из одного звена и стойки. В теме 3 такая кинематическая цепь названа начальным механизмом I класса. Тогда уравнение движения механизма можно заменить тождественным ему уравнением движения одного звена, называемого звеном приведения.

Звено приведения — одно из звеньев исследуемого механизма, имеющее ту же скорость, что и в реальном механизме. Если звено приведения — вращающееся (кривошип, рис. 7.2), то оно будет обладать приведенным моментом инерции I_п и на него действует приведенный момент сил .

Поступательно движущееся звено приведения (ползун, рис. 7.3) обладает приведенной массой , и на него действует приведенная сила .

NB 7.1. Для облегчения динамических расчетов механизм с n звеньями заменяют одномассовой динамической моделью, состоящей из одного звена и стойки.

NB 7.2. Звено приведения должно обладать приведенным моментом инерции I_п(приведенный массой m_п), к нему прикладывают приведенный момент сил M_п (приведенную силу F_п).

NB 7.3. Приведенные силы и моменты сил являются эквивалентом всех сил, действующих на звенья механизма, а приведенные массы и моменты инерции — эквивалентом инертности механизма.