Учебное пособие по курсу "Теория механизмов и машин", страница 60

При третьем пуске (рис. 9.7, в) находят амплитуду  колебаний, вызванных теми же факторами, но с грузом , установленным в диаметрально противоположной точке, по выражению:

                                                                    (9.22)

Параллелограммы амплитуд на рис. 9.7, б и в равны, как имеющие равные стороны и углы. Амплитуды А₁ и А₂ являются диагоналями параллелограммов. Из теоремы о равенстве суммы квадратов диагоналей сумме всех четырех сторон параллелограмма:  — находят величину амплитуды :

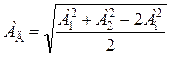                                   .                        (9.23)

Из формулы (9.20) находят коэффициент пропорциональности:

                                           .                                (9.24)

По амплитуде начального дисбаланса  и коэффициенту  определяют величину начального дисбаланса:

                                  .                        (9.25)

Такой же дисбаланс должен иметь противовес, устанавливаемый на диске A, т.е. . Задаваясь массой противовеса , рассчитывают положение противовеса на диске A относительно центра вращения:

                                    .                                  

Для определения углового положения противовеса рассматривают векторный параллелограмм (рис. 9.8). По теореме косинусов:

              ,                     откуда

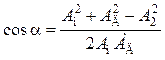                                   .                        (9.26)

Одному значению cosa соответствуют два значения a. Действительный угол a определяют опытным путем. Устанавливая противовес поочередно в четырех точках (рис. 9.9) на рассчитанном расстоянии r_п, определяют амплитуду остаточного дисбаланса А₀₁, А₀₂, А₀₃, А_04. Наименьшая амплитуда определит место установки противовеса.

Для определения дисбаланса D_B  ротор 1 (см. рис. 9.5) снимают с подшипников 2 рамы 3, поворачивают вокруг вертикальной оси и вновь устанавливают на подшипники так, чтобы с осью шарнира 4 на этот раз была совмещена плоскость коррекции A. Путем пробного и дополнительных пусков определяют параметры противовеса в плоскости B: m_B, r_B и a_B. В плоскостях коррекции навешивают грузы с массами m_A и m_B. Нетрудно заметить, что и в данном случае динамическую балансировку выполняют крестом векторов противовесов, устанавливаемых в параллельных плоскостях.

9.8. Статическое уравновешивание масс диадных механизмов

9.8.1. Шарнирный четырехзвенник

При уравновешивании масс плоских механизмов часто ограничиваются условием (9.6):

Это условие выполняется лишь в том случае, когда центр тяжести S системы подвижных звеньев механизма не перемещается, а занимает постоянное положение. Достичь этого можно с помощью метода заменяющих масс.

Пусть дано тело АВ массой m (рис. 9.10), совершающее плоское или вращательное движение. Сосредоточим массу тела, распределенную по всему объему, в точках А и В. Значения сосредоточенных масс m_А и m_В определяют из уравнений:

                                         ;                               (9.27)

                                         .                              (9.28)

Уравнение (9.27) очевидно: масса заменяющей системы равна массе заданного тела. Уравнение (9.28) означает, что центр тяжести системы S располагается в том же месте, что и центр тяжести S заданного тела. Отсюда следует, что главный вектор сил инерции заменяющей системы  равен главному вектору сил инерции заданного тела. Такая замена каждого звена двумя сосредоточенными массами корректна применительно только к статическому уравновешиванию.

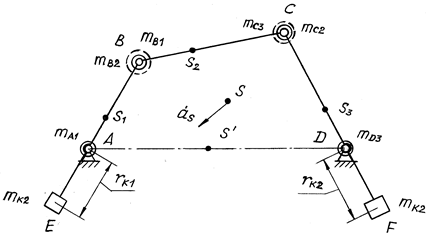
Рис. 9.11

В шарнирном четырехзвеннике АВСD (рис. 9.11) заданы: длины подвижных звеньев l₁, l₂, l₃, их массы m₁, m₂, m₃ и положения центров тяжести S₁, S₂, S₃. Каждое звено заменяют двумя сосредоточенными массами, используя уравнения (9.27) и (9.28). Массу m₁ звена длиной l заменяют двумя массами, сосредоточенными в точках А и В, причем для решения задачи необходима только масса, сосредоточенная в точке В, так как масса m_А сосредоточена в центре вращения. Из системы уравнений (9.27) и (9.28) находят заменяющие массы: