Учебное пособие по курсу "Теория механизмов и машин", страница 111

16.6. Синтез кулачкового механизма по углу передачи

Отрезок ВК = ОD откладывают перпендикулярно к траектории точки В. Если соединить точки О и К, то можно отметить следующий результат: в любом положении механизма луч ОК составляет с перпендикуляром к соответствующему вектору _qB в точке К угол давления J.

Из рис. 16.10, а видно, что луч ОК проведен под углом передачи m к вектору аналога скорости. Из построений можно вывести правило центра вращения кулачка:

NB 16.3. Если из конца вектора аналога скорости, приложенного в центре ролика В, провести луч под углом передачи m к вектору υ_qB, то он пройдет через центр вращения кулачка.

Так как этот вывод справедлив для любого положения толкателя, то его можно использовать для нахождения центра вращения кулачка при параметрическом синтезе механизма.

Лекция № 25

16.7. Определение основных размеров кулачка

16.7.1. Исходные данные и задачи синтеза

Задано: фазовые углы φ_у, φ_д, φ_с, φ_б;

максимальное перемещение толкателя S_max;

допускаемые углы давления в фазах удаления  = 30⁰ и сближения  = 45⁰; функция аналога ускорения a_qB = a_qB(φ₁).

Первая часть решения задачи: определение зависимостей перемещений толкателя S_В = S_В(φ₁) и аналога скорости _qB = _qB(φ₁).

Вторая часть: определение начального (минимального) радиуса r_о и смещения e. Смещение во внецентренном механизме определяют как кратчайшее расстояние от центра вращения кулачка до траектории движения толкателя. При e = 0 механизм называется центральным.

16.7.2. Графический метод

Чтобы охватить все положения кулачкового механизма, необходимо для каждого положения точки В (для каждого значения φ₁) найти соответствующий вектор аналога скорости _qB и отложить его в масштабе перпендикулярно направлению движения толкателя. Условно принято, что при вращении кулачка по часовой стрелке и движении толкателя вверх (т.е. в фазе удаления) отрезки u_qB откладывают вправо, а в фазе сближения — влево. Объединив концы всех отрезков u_qB, получают диаграмму u_qB = u_qB (S).

Построение кинематических диаграмм движения толкателя проиллюстрировано на рис. 16.8. В качестве примера рассмотрен косинусоидальный закон изменения аналога ускорения .

Графическим интегрированием (см. тему 8) диаграммы  получают зависимость аналога скорости по углу поворота _qB = = _qB (φ₁) (рис. 16.8, б). Повторное интегрирование дает диаграмму линейных перемещений S_В = S_В(φ₁) (рис. 16.8, в).

Диаграмму аналога ускорений строят в произвольном масштабе, который рассчитывают после двухкратного дифференцирования. По оси абсцисс откладывают рабочий фазовый угол φ_1p в масштабе (мм/рад):

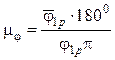                                        ,                              (16.8)

где _1p — отрезок, изображающий рабочий фазовый угол, мм; φ_1p — рабочий фазовый угол, град, см. формулу (16.2).

Фазовые углы в фазах удаления φ_у и сближения φ_с делят на определенное число участков (в курсовом проекте рекомендуется делить на 6 частей). Масштаб диаграммы перемещений в мм/рад:

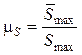                                           ,                                 (16.9)

где — максимальная ордината диаграммы , мм.

Масштаб аналога скоростей в мм/мм:

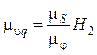                                          ,                              (16.10)

где Н₂ — отрезок повторного интегрирования, мм.

Масштаб скорости, мм/(м ∙ с^-1):

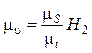                                          ,                               (16.11)

где m_t — масштаб времени, мм/с, формула (4.24),

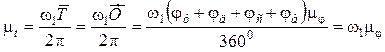             , (16.12)

где ω₁ — угловая скорость кулачка, с^-1.

Построения для определения основных размеров кулачка удобно вести при одинаковых масштабах μ_S и μ_υq. Принимая в формуле (16.10) μ_υq = μ_S, рассчитывают отрезок интегрирования:

                                              Н₂ = m_φ.                                            

Для определения основных размеров механизма в масштабе m_S строят диаграмму  = (), откладывая отрезки , соответствующие отрезкам , перпендикулярно траектории движения толкателя и соединяя концы этих отрезков (рис. 16.9, г).