Учебное пособие по курсу "Теория механизмов и машин", страница 24

Метод кинематических диаграмм дает наглядную картину кинематических параметров за полный цикл движения начального звена. Однако в отличие от планов скоростей и ускорений, полная картина дается только для одной точки, движущейся поступательно.

Диаграммы скоростей и ускорений могут быть получены также методом графического дифференцирования.

В рассмотренном механизме исследуемая точка С движется прямолинейно. Для точек, имеющих криволинейное движение, строят кинематические диаграммы в полярной системе координат. Для этого векторы скоростей и ускорений, например _s2 и a_s2 шатуна, изображают в их истинном направлении. На этих направлениях в масштабе откладывают отрезки, изображающие кинематические параметры во всех положениях кривошипа. Соединяя концы всех векторов плавной кривой, получают годограф скорости или годограф ускорения. Образец годографа скорости точки S₂ шатуна приведен на рис. 4.6.

4.5. Графическое дифференцирование. Метод секущих (метод хорд)

Принцип графического дифференцирования известен из курса высшей математики. Он предложен Л.П. Смирновым. Один из его методов носит название «метод секущих» (метод хорд). Для иллюстрации метода на рис. 4.7 изображен фрагмент рис. 4.2. Метод состоит в том, что криволинейную диаграмму заменяют ломаной, когда на каждом участке кривую заменяют прямой (хордой), стягивающей ее. При заданной функции  хорда 9–8^о (рис. 4.7,  а) образует с осью абсцисс угол φ.

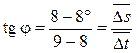                                      .                            (4.36)

При Δt = 0 формула (4.36) имеет вид:

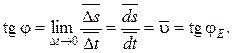                                                (4.37)

Следовательно, при малости промежутка Δt можно считать, что формула (4.37) дает значение средней скорости, т.е. скорости точки Е, расположенной посередине отрезка 9–8.

От начала координат 9 будущей диаграммы скоростей (рис. 4.7, б) откладывают влево произвольный отрезок , называемый отрезком дифференцирования. Его длину принимают произвольно, но с учетом размеров строящегося графика. Рекомендуется Н₁ = 40…60 мм.

Из точки P₁ (полюса дифференцирования) проводят луч  параллельно хорде 9–8^о до пересечения с осью ординат в точке 8¢. Из D следует:

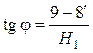                                          .                                (4.38)

С учетом формул (4.37) и (4.38) можно записать:

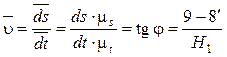                             ,                            откуда

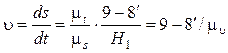                             .                   (4.39)

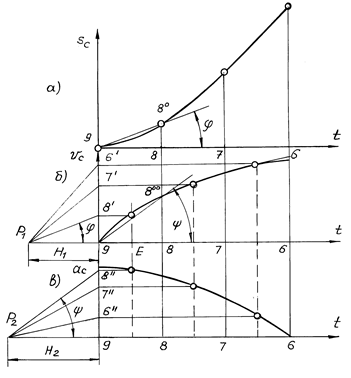
Рис. 4.7

Масштаб диаграммы скоростей, мм/(м·с^-1), из формулы (4.39):

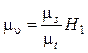                                           .                                 (4.40)

Таким образом, отрезок 9– в масштабе  действительно изображает скорость на середине участка 9–8.

NВ 4.13. Луч, проведенный из полюса  параллельно хорде участка кривой , отсекает на оси ординат отрезок, изображающий в масштабе  скорость на середине участка.

На диаграмме  (см. рис. 4.7, б) отрезок 9– откладывают на середине участка 9–8. Проводя из полюса ряд лучей, параллельных секущим, откладывают ординаты на серединах участков и соединяют их плавной кривой, получая диаграмму u_С = = _С (t). Кривую вычерчивают с помощью лекала. Для определения величины скорости в заданном положении кривошипа, например, в положении 8, необходимо ординату диаграммы (8–8^оо) поделить на масштаб.

Аналогично строят диаграмму  путем графического дифференцирования диаграммы . Отрезок повторного дифференцирования 9 – Р₂ = Н₂ (рис. 4.7, в) назначают также произвольно. Луч , проведенный параллельно хорде 9–8^¢¢, стягивающей кривую _C на участке 9–8, отсекает на оси ординат отрезок, изображающий ускорение а_С посередине участка. Другие лучи —  и  — отсекают отрезки, изображающие ускорения точки С посередине участков 8–7 и 7–6, и т.д. Из построений на рис. 4.7, б, в следует:

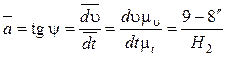                             ,                            откуда

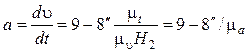                           .                 (4.41)

Масштаб диаграммы ускорений, мм/(м·с^-1):

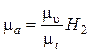                                           .                                 (4.42)