В формулу (13.1) подставлены p1 = 3, равное числу вращательных пар, и p2 = 2, равное числу зубчатых зацеплений (z1/z2 и z2/z3), являющихся высшими парами. Из этой же формулы следует, что механизм может иметь одно ведущее звено. Обычно таким является либо солнечное колесо 1, либо водило h, а также колесо 3 при закрепленном колесе 1. Конструкция, в которой предусмотрена возможность затормаживания одного или другого центрального колеса, является двухступенчатой коробкой скоростей.
Аналитические кинематические соотношения в планетарных механизмах гораздо проще, чем в рычажных механизмах, однако сложнее, чем в зубчатых механизмах с неподвижными осями. Вывод таких соотношений производится с использованием метода обращения движения (метода Виллиса). Известные кинематические соотношения из формул (12.1) и (12.2) могут быть использованы только при неподвижных осях колес.
NB 13.2. По методу обращения движения системе звеньев сообщается движение со скоростью, равной скорости одного из звеньев, но с противоположным знаком. Такое звено будет условно неподвижным.
В планетарном механизме подвижные оси можно
условно остановить, задавая всем звеньям механизма вращательное движение с
угловой скоростью ![]() (верхний индекс указывает неподвижное
звено). При этом водило остановится, а звено 3 начнет вращаться.
Образованный при этом обращенный механизм представляет собой обычный
двухступенчатый редуктор с двумя зацеплениями: z1/z2
и z2/z3, для которого нетрудно определить
передаточное отношение, выраженное через числа зубьев. Угловые скорости звеньев
планетарного и обращенного механизмов приведены в табл. 13.1.
(верхний индекс указывает неподвижное
звено). При этом водило остановится, а звено 3 начнет вращаться.
Образованный при этом обращенный механизм представляет собой обычный
двухступенчатый редуктор с двумя зацеплениями: z1/z2
и z2/z3, для которого нетрудно определить
передаточное отношение, выраженное через числа зубьев. Угловые скорости звеньев
планетарного и обращенного механизмов приведены в табл. 13.1.
Таблица 13.1
Номер звена |
Планетарный механизм |
Обращенный механизм |
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
h |
|
|
Нетрудно видеть, что в последней колонке таблицы угловые скорости звеньев обращенного механизма определяют вычитанием угловой скорости водила из угловых скоростей звеньев планетарного механизма. Передаточное отношение обращенного механизма:
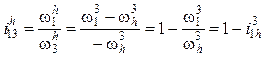 , откуда передаточное отношение
планетарного механизма:
, откуда передаточное отношение
планетарного механизма:
![]() .
(13.2)
.
(13.2)
NB 13.3. Формула Виллиса:
Передаточное отношение планетарного механизма, рассчитанное от зубчатого колеса к водилу, равно единице минус передаточное отношение обращенного механизма.
По формуле Виллиса можно рассчитать передаточное отношение любого планетарного механизма, а также угловые скорости всех звеньев. С использованием формул (12.1) и (12.2) формула (13.2) примет вид:
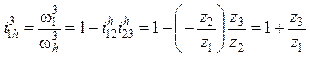 . (13.3)
. (13.3)
В формуле
(13.3) использованы: знак «минус» - для
внешнего зацепления z1/z2 и знак «плюс» —
для внутреннего z2/z3. Из нее следует, что
так как числа зубьев положительные, то передаточное отношение ![]() всегда положительное, а звенья 1 и
h вращаются в одном направлении. Из формулы (13.3) можно определить угловую
скорость водила:
всегда положительное, а звенья 1 и
h вращаются в одном направлении. Из формулы (13.3) можно определить угловую
скорость водила:
![]() .
(13.4)
.
(13.4)
Аналогично по формуле Виллиса может быть определена угловая скорость сателлита, необходимая для расчета его подшипников:
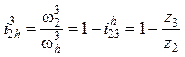 , откуда
, откуда
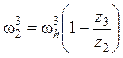 . (13.5)
. (13.5)
Особенностью формулы Виллиса является то, что в индексе передаточного отношения буква h всегда стоит на втором месте. При необходимости определения передаточного отношения от водила к центральному колесу формула Виллиса может быть использована после инверсии:
![]() .
(13.6)
.
(13.6)
Коэффициент полезного действия редуктора Джеймса зависит от направления движения и определяется по формулам [20]:
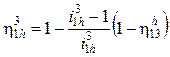 , (13.7)
, (13.7)
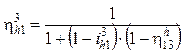 . (13.8)
. (13.8)
В формулах
(13.7) и (13.8) ![]() — КПД ряда зубчатых колес,
— КПД ряда зубчатых колес,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.