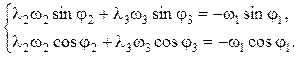Учебное пособие по курсу "Теория механизмов и машин", страница 29

                                  (5.20)

Корни уравнений (5.20) находят по формуле Крамера.

NB 5.3. Определитель системы линейных уравнений составляют из коэффициентов при неизвестных:

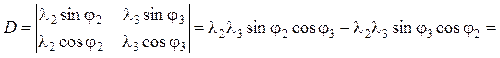
                                                                (5.21)

Определители D₂ и D₃ получают из D путем замены столбцов с коэффициентами при искомых членах столбцами, составленными из свободных членов:

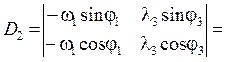
                                                              (5.22)

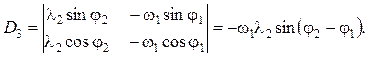                    (5.23)

Корни системы:

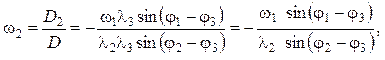                  (5.24)

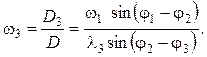                                                    (5.25)

Знак угловой скорости определяет ее направление: плюс — против часовой стрелки, минус — по часовой стрелке. Линейные скорости точек кривошипа и коромысла:

                                  (5.26)

Линейные скорости направлены перпендикулярно звеньям в сторону вращения. Угол вектора скорости коромысла рассчитывают с учетом направляющего угла φ₃ коромысла 3 и знака угловой скорости (рис. 5.3 и табл. 5.1).

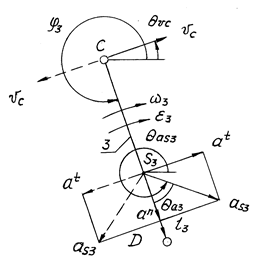
Рис. 5.3

Таблица 5.1

Векторы скоростей перпендикулярны звену 3 и направлены в сторону вращения (по направлению угловой скорости w₃).

5.3.4. Определение ускорений

Для определения угловых ускорений звеньев выполняют дифференцирование системы (5.19):

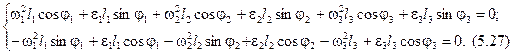
После введения коэффициентов длины l, перемещения известных величин в правую часть уравнения в качестве свободного члена и принятия e₁ = 0 (так как w₁ = const) получают:

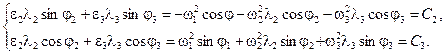    (5.28)

Определители для расчета корней системы:

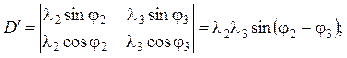                        (5.29)

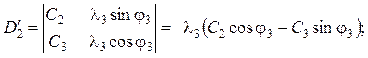                    (5.30)

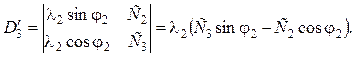                        (5.31)

Корни системы:

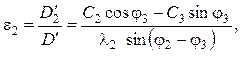                                              (5.32)

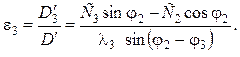                                              (5.33)

Линейные ускорения:

              (5.34)

Ускорение точки B при равномерном вращении — нормальное (центростремительное), направлено по звену BA к центру вращения A. В точках C и S₃ прикладывают две составляющие ускорения: нормальную, направленную к центру вращения D, и тангенциальную, перпендикулярную нормальному ускорению, направленную в сторону углового ускорения e₃. Острый угол q_a3 между звеном 3 и векторами a_C и a_S3 составляет:

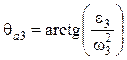                                       ,                             (5.35)

а угол между осью x и направлением вектора результирующего ускорения в соответствии с рис. 5.3 и табл. 5.2:

                                                                          (5.36)

Таблица 5.2

5.3.5. Определение параметров центра масс шатуна

Координаты центра масс  шатуна, расположенного на расстоянии  от точки B (рис. 5.2), определяют по формулам:

                                                  (5.37)

                               .                    (5.38)

Дифференцированием уравнений (5.37) и (5.38) получают выражения для проекций скоростей точки S₂ на координатные оси:

                        ,              (5.39)

                                            (5.40)

Результирующая скорость

                                   .                         (5.41)

Ее направление определяют по формуле

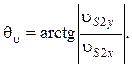                                                                    (5.42)

В результате повторного дифференцирования получают проекции ускорений точки S₂ на координатные оси, полное ускорение и угол его расположения:

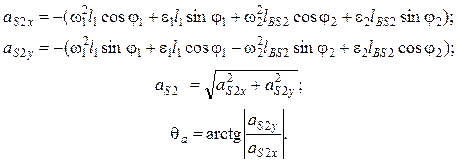   (5.43)

Углы расположения векторов  и  к положительному направлению оси x связаны не только θ, но и со знаками проекций (рис. 5.2 и 5.4) и определяются по табл. 5.3.

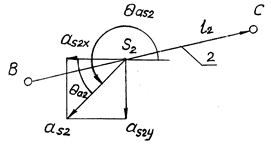
Рис. 5.4

Таблица 5.3