А0-2 = А0-1 + А1-2. (8.18)
Работы на других участках определяют аналогично. Правило трапеций использовано в программе ТММ-1, составленной в системе Quick BASIC для определения момента инерции маховика механизма ДВС (см. рис. 3.2); описание программы приведено в методике [8].
Пример 8.1. Рассчитать методом численного интегрирования диаграммы моментов работу в точках 2, 1 и 12, если задано: моменты М3 = 0; М2 = –118 Н∙м; М1 = 425 Н∙м; М12 = 1168 Н∙м.
Решение:
А) Угловой шаг Δφ = 2π/12 = 0,5236 рад.
Б) Работа в точке 2, равная приращению работы на участке 3–2, — формула (8.17):
А2 = 0,5(М3 + М2)Δφ = 0,5∙ (–118) ∙0,5236 = –30,9 Дж.
В) Приращение работы на участке 2–1:
A2-1 = 0,5(М2 + М1)Δφ = 0,5∙ (–118 + 425) ∙0,5236 = 80,4 Дж.
Работа в точке 1:
А1 = А2 + А2-1 = –30,9 + 80,4 = 49,5 Дж.
Г) Приращение работы на участке 1–12:
А1-12 = 0,5(М1 + М12) Δφ = 0,5∙(425+1168)∙0,5236 = 417 Дж.
Работа в точке 12:
А12 = А1 + А1-12 = 49,5 + 417 = 466,5 Дж.
|
Рис. 8.5 |
Примечание. Исходные данные взяты из компьютерной распечатки по программе ТММ-1 приведенных моментов сил рычажного механизма ДВС по данным варианта 18 [8], которые определяют по равенству Мп = –Му. Эти данные и распечатка работ AД, рассчитанных по правилу трапеций (8.14), представлены на рис. 8.5.
Вывод:
Результаты компьютерных и «ручных» расчетов совпадают с высокой точностью.
В соответствии с уравнением (7.4) в установившемся режиме за цикл (за полный оборот кривошипа) работа движущих сил равна работе сил сопротивления, т.е. в начале первого и в конце последнего участка АД = AC.
При условии постоянства момента движущих сил МД диаграмму работ движущих сил АД строят соединением первой и последней точек кривой АС = AC(j) прямой линией — линия IV (рис. 8.3, в). График МД = МД(φ) строят методом графического дифференцирования (см. тему 4). Для этого из полюса Р1 проводят луч, параллельный прямой АД = АД(j) до пересечения с осью ординат. Прямая V на рис. 8.3, б (штриховая), параллельная оси абсцисс, и является графиком МД = МД(φ).
Приращение кинетической энергии за цикл DT = 0 — в соответствии с формулой (7.4). Однако в любой другой момент времени выполняется равенство (7.1): приращение кинетической энергии
.
(8.19)
График избыточных работ Аизб (приращение кинетической энергии ΔТ — кривая VI на рис. 8.3, г) строят вычитанием АС из АД (отрезки вдоль оси ординат между диаграммами АД = АД(φ) и АС = АС(φ)).
Приведенный момент инерции определяют из условия равенства кинетической энергии звена приведения сумме кинетических энергий всех звеньев механизма. Для кривошипно-ползунного механизма (см. рис. 8.2) формула приведенного момента (7.13) запишется так:
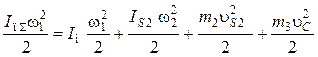, (8.20)
где IпS — суммарный приведенный момент инерции, кг∙м2; Iм — момент инерции маховика, искомый параметр динамического синтеза.
Из формулы (8.20) следует:
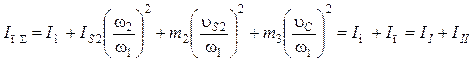, (8.21)
где 
—
приведенный момент инерции всех звеньев, кроме
начального; величина 
— переменная, она определяется
тремя последними слагаемыми выражений (8.20)
и (8.21); 
— момент инерции звена 1,
включающий момент инерции маховика, значительно превышающий другие слагаемые,
момент инерции кривошипа и других связанных с ним элементов, например, зубчатого
колеса (см. рис. 8.2); величина 
— постоянная.
Диаграмму 
— график VII на рис. 8.3, д
— строят в масштабе 
, мм/(кг∙м2):
,
(8.22)
где 
—
отрезок, изображающий максимальную величину приведенного момента инерции, мм.
Диаграмма с началом координат в точке О одновременно
является диаграммой 
кинетической энергии всех
звеньев, кроме звена приведения, — график VIII на рис. 8.3, д. Это следует из выражения
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
