Учебное пособие по курсу "Теория механизмов и машин", страница 83

Таблица 14.1

Выбрав начальную точку эвольвенты М_о, проводим начальный радиус-вектор r_b. Далее под эвольвентными углами _y к нему откладываем текущие радиусы-векторы r_y. Соединяя концы текущих радиусов-векторов, получаем правую ветвь эвольвенты (рис. 14.4).

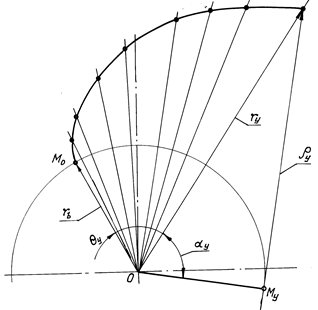
Рис. 14.4

Лекция № 19

14.5. Делительная окружность

Кроме основного закона зацепления — обеспечения заданного постоянного передаточного отношения — при проектировании зацепления должны быть выполнены дополнительные условия синтеза.

Выполнение дополнительных условий зависит в первую очередь от размеров зубьев. Их удобно задавать в долях какой-либо одной величины, связанной с зубом. Для пояснения выбора этой величины выражают длину некоторой окружности, имеющей диаметр d (рис. 14.5), через число зубьев колеса:

                                              pd = pz,                                  (14.14)

где р — окружной шаг; это расстояние, измеренное по дуге окружности между двумя одноименными профилями соседних зубьев. Из формулы (14.14) следует:

                                                                                           или

                                              d = m z,                                  (14.15)

где m — отношение окружного шага к p, называемое модулем зуба.

                                              ,                                             отсюда шаг

                                              p = p m.                                  (14.16)

NB 14.6. Модуль — линейная величина, в  раз меньшая окружного шага зубьев.

Окружной шаг p и модуль m для одного и того же зуба зависят от диаметра окружности, к которой они относятся. Для некоторой окружности, принимаемой за базовую для определения размеров зубьев и их элементов и называемой делительной, выбирают модуль в пределах от 0,05 до 100 мм по ГОСТ 9563-60. В общем машиностроении применяют модули 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10 мм и другие, имеющие большие значения.

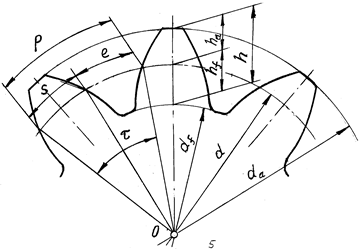
Рис. 14.5

Модуль m является одной из основных величин, характеризующих размеры зуба. В соответствии с формулой (14.16) при стандартном модуле шаг будет также иметь стандартную величину. Окружность, диаметр которой определяют по формуле (14.15) при стандартном модуле, называют делительной.

NB 14.7. Делительной называется окружность, для которой модуль имеет стандартную величину.

В нулевых зацеплениях начальные и делительные окружности совпадают, но они имеют принципиальное различие. Делительная окружность есть характеристика одного зубчатого колеса, с которым она неизменно связана, и диаметр этой окружности имеет постоянную величину — формула (14.15). Начальные окружности дают характеристику зацепления двух зубчатых колес, и диаметры этих окружностей зависят от межосевого расстояния (рассматривается далее в п. 14.12).

14.6. Исходные контуры

Ввиду широкого применения зубчатых передач стандартизированы многие их показатели. В частности, ГОСТ 16530-83 и ГОСТ 16531-83 регламентируют термины, определения и обозначения цилиндрических зубчатых передач.

Делительная окружность в торцовом сечении делит зуб на две части: головку и ножку (рис. 14.5). Головкой называют часть зуба, расположенную между делительной окружностью и окружностью вершин диаметра d_a. Высоту головки обозначают h_a:

                                            .                                (14.17)

Значения коэффициента высоты головки зуба  и других коэффициентов при модуле регламентируются стандартом на исходный контур (для цилиндрических передач — ГОСТ 13755-81).