Учебное пособие по курсу "Теория механизмов и машин", страница 67

Изображаем ползун в положениях С₁ и С₂ на расстоянии H = = 80 мм. В середине отрезка С₁С₂ восстанавливаем перпендикуляр. Из точки С₁ проводим луч под углом  к перпендикуляру до пересечения с ним в точке О. Радиусом ОС₁ описываем окружность расположения центра вращения кривошипа. В точке С₁ восстанавливаем еще один перпендикуляр к отрезку С₁С₂. Из точки С₁ проводим к нему луч под углом  до пересечения с окружностью в точке A.

Длины отрезков:

                               AС₁ = 42 мм, AС₂  = 114 мм.                             

Длины звеньев:

l₁ = (114 – 42)/2 = 36 мм; l₂ = 114 – 36 = 78 мм.

Смещение

                             e = (78 – 36)sin 45^о = 29,7 мм;                            графическая проверка: e = 30 мм.

Вывод:

Аналитические и графические результаты совпадают.

10.8. Синтез механизма поперечно-строгального станка по коэффициенту изменения средней скорости и углу передачи^*

В механизме поперечно-строгального станка (рис. 10.12) вращательное движение кривошипа 1 преобразуется в возвратно-поступательное движение ползуна 5. В режиме рабочего хода осуществляется технологический процесс резания с определенной скоростью, а холостой ход производится с большей средней скоростью. Такая неравномерность движения выходного звена, как и при вращательном движении, характеризуется коэффициентом изменения средней скорости:

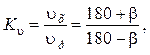                                                              (10.19)

откуда угол размаха кулисы

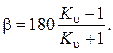                                                                      (10.20)

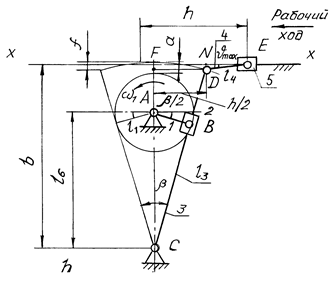
Рис. 10.12

Значения коэффициента задают в пределах: K = 1,3…1,4. Длину кулисы рассчитывают из прямоугольного DCDF:

                                                        (10.21)

При расположении кулисы 3 в среднем положении выполняется равенство:

                                                                       (10.22)

где  — длина стойки;  — длина кривошипа; a — конструктивный размер; выбирают с целью наиболее полного использования длины кулисы.

Длина кулисы из прямоугольного DABC:

                                                                      (10.23)

После подстановки значения  в выражение (10.22) получают длину стойки:

                                                     (10.24)

После расчета  определяют  по формуле (10.23); для данных механизмов принимают  В механизме при вращении кривошипа угол давления  так как реакция  и скорость  совпадают по направлению. Для обеспечения наименьших углов давления  положение оси x–x принимают так, чтобы она делила стрелку сегмента f пополам. Из DNDE следует:

                                                        (10.25)

Длина стрелки сегмента

                                                              (10.26)

При выполнении условия (10.25) будет обеспечено Расстояние между осью вращения и осью направляющей ползуна 5:

                                                                         (10.27)

10.9. Синтез механизма с качающимся цилиндром

10.9.1. Синтез по минимальному углу давления

Механизм с возвратно-качающимся цилиндром применяют в гидро- и пневмоприводах различных машин, в том числе строительных и путевых. Исходные данные: длина коромысла , размах β, допускаемый угол давления  и конструктивный коэффициент k. Рассчитать: ход поршня h, минимальную длину цилиндра  и длину стойки .

На рис. 10.13 механизм изображен в крайних положениях коромысла  и  c размахом β. Ход поршня  определяют по формуле:

                                       .                          (10.28)

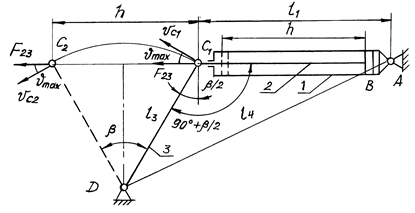
Рис. 10.13

На продолжении прямой откладывают отрезок  Коэффициент k = 1,3; 1,4 и т.д. В крайних положениях в точках  и  угол давления определяют как угол между осью цилиндра и вектором скорости  точки приложения силы:

                                      .                         (10.29)

В остальных положениях угол давления будет меньше, поскольку при переходе точки C из положения  в положение  он меняет свой знак и, следовательно, проходит через нулевое значение.