Машиностроение \ Теории механизмов и машин

Учебное пособие по курсу "Теория механизмов и машин", страница 74

Задача № 53 (рис. 12.9)

Рис. 12.9

Рассчитать передаточное отношение каждой ступени сложного зубчатого механизма и общее передаточное отношение i14, общий КПД h14, если КПД одного зубчатого зацепления h = 0,96. Рассчитать угловую скорость ведомого звена w4. Вычертить кинематическую схему.

Параметр

Вариант

1

2

3

Числа зубьев     z1

18

20

22

z2

38

45

50

19

22

25

z3

56

68

78

24

26

28

z4

82

88

92

Угловая скорость w1, с-1

100

120

140

Задача № 54 (рис. 12.10)

Рассчитать передаточное отношение каждой ступени сложного зубчатого механизма и общее передаточное отношение i14, общий КПД h14, если КПД одного зубчатого зацепления h = 0,96. Рассчитать угловую скорость ведомого звена w4. Вычертить кинематическую схему.

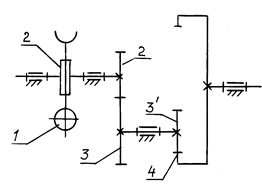
Рис. 12.10

Параметр

Вариант

1

2

3

Числа зубьев   z1

1

2

4

z2

40

70

60

18

20

22

z3

80

90

100

20

24

28

z4

110

115

120

Угловая скорость w1, с-1

170

190

210

КПД червячной передачи hч

0,75

0,85

0,9

Задача № 55 (рис. 12.11)

Рассчитать передаточное отношение каждой ступени сложного зубчатого механизма и общее передаточное отношение i14, общий КПД h14, если КПД одного зубчатого зацепления h = 0,96. Рассчитать угловую скорость ведомого звена w4. Вычертить кинематическую схему.

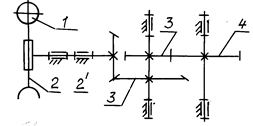
Рис. 12.11

Параметр

Вариант

1

2

3

Числа зубьев    z1

1

2

4

z2

46

58

62

18

20

22

z3

40

45

50

20

22

24

z4

82

90

96

Угловая скорость w1, с-1

140

160

180

КПД червячной передачи hч

0,72

0,84

0,91

Лекция № 17

Тема 13: Зубчатые передачи с подвижными осями

13.1. Планетарные механизмы

13.1.1. Редуктор Джеймса

Передачи вращения, у которых одна или несколько осей вращения зубчатых колес подвижны, называются планетарными либо дифференциальными. Наибольшее распространение получили планетарные зубчатые механизмы. Самый распространенный — простой планетарный редуктор (рис. 13.1), или редуктор Джеймса.

Он состоит из трех подвижных звеньев 1, 2, h и стойки, с которой соединено колесо с внутренними зубьями 3. Колеса 1 и 3 — центральные, причем колесо 1 — солнечное, а колесо 3 — корончатое. Колеса 2 с подвижными геометрическими осями называют сателлитами. Планетарный механизм имеет один или несколько сателлитов. Отличительной особенностью планетарных и дифференциальных механизмов является наличие рычажного звена h, называемого водилом, в котором установлены сателлиты.

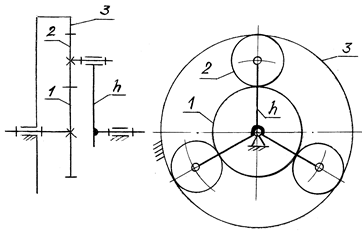
Рис. 13.1

NB 13.1. Планетарным называется зубчатый механизм с подвижными осями, в котором одно из колес — неподвижное.

Основными звеньями данного планетарного механизма являются два центральных колеса (2k) и водило (h), поэтому редуктору Джеймса по классификации В.Н. Кудрявцева [18] присваивают обозначение 2k-h. Число степеней свободы по формуле Чебышева (с учетом одного сателлита):

                         W = 3n – 2p1 – p2 = 3×3 – 2×3 – 2 = 1.               (13.1)

Скачать файл