На рис. 4.2, б, в, г показан процесс графического дифференцирования и повторного дифференцирования для определения скоростей и ускорений точки С ползуна кривошипно-ползунного механизма. Приведенные построения позволяют вывести важное правило правильности выполнения графического дифференцирования.
NB 4.14. Максимуму диаграммы скоростей соответствует нуль на диаграмме ускорений, и наоборот, максимальным ускорениям соответствуют нулевые скорости.
Метод графического дифференцирования не является достаточно точным. При повторном и тройном дифференцировании он становится практически непригодным. Как правило, он применяется в прикидочных и ориентировочных расчетах. Намного точнее метод численного дифференцирования.
Численное дифференцирование функции, например s = s(t), выполняется, если она задана в виде массива чисел sn, sn+1, sn+2 и т.д., рассчитанных или заданных через равные интервалы времени Δt, например, Т/12. Чем меньше шаг Δt, тем точнее можно вычислить значение производной функции. Среднюю скорость как первую производную перемещения определяют по формуле:
. (4.43)
Эта формула идентична формуле (4.36) графического дифференцирования, которая определяет среднюю скорость на участке как тангенс угла φ (рис. 4.7).
В современных прикладных программах на ПЭВМ, например, MathCAD, используются более сложные интерполяционные соотношения с высокой точностью результатов, которые также зависят и от точности исходных данных.
Пример 4.6. Рассчитать методом численного дифференцирования диаграммы перемещений величины средних скоростей на участках 9–8, 8–7, 7–6 и в точках 8 и 7 (рис. 4.7), если задано: угловая скорость начального звена ω1 = 215 с-1, перемещения s9 = 0; s8 = 0,008 м; s7 = 0,032 м; s6 = 0,069 м.
Решение:
1. Время одного оборота кривошипа:
t = 2π/ω1 = 2π/215 = 0,0292 с.
Время перемещения кривошипа на одно положение:
Dt = t/12 = 0,0292/12 = 0,0024 с.
2. Средняя скорость на участке 9–8 — формула (4.43):
9-8 = (s8
– s9)/∆t = 0,008/0,0024 = 3,28 м/с.
3. Средняя скорость на участке 8–7:
8-7 = (0,032
– 0,008)/0,0024 = 9,85 м/с.
4. Средняя скорость на участке 7–6:
7-6 = (0,069
– 0,032)/0,0024 = 15,19 м/с.
5. Линейная интерполяция для точек 1 и 2 дает следующие результаты:
8
= (9-8 + 8-7)/2
= (3,28 + 9,85)/2 = 6,57 м/с;
7
= (8-7 + 7-6)/2
= (9,85 + 15,19)/2 = 12,52 м/с.
Примечание.
Исходные данные взяты из компьютерной распечатки (рис. 4.8) перемещений ползуна
С рычажного механизма ДВС по программе ТММ-1 по данным
варианта 18 [8]. По этим данным, 8 = 6,6 м/с, 7 = 12,9 м/с.
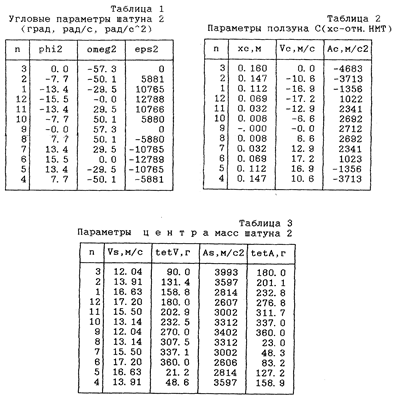
Рис. 4.8
Вывод:
Отклонения компьютерных и «ручных» расчетов составляют 0,45 % и 2,9 % соответственно, что приемлемо.
1. Цель кинематического анализа — определение положений, скоростей и ускорений звеньев механизма.
2. Кинематический анализ выполняют двумя методами: аналитическим и графическим.
3. Графический метод кинематического анализа подразделяется на методы планов и кинематических диаграмм.
4. Скорость — первая производная от перемещения по времени, ускорение — вторая производная от ускорения по времени.
5. Аналог скорости — первая производная от перемещения от угла поворота кривошипа, аналог ускорения — вторая производная.
6. План положений — кинематическая схема механизма, выполненная в масштабе.
7. Масштаб определяют отношением длины отрезка, изображающего физическую величину, к самой физической величине.
8. Для определения длины отрезка, откладываемого на плане, физическую величину умножают на масштаб.
9. Для определения физической величины длину отрезка на чертеже делят на масштаб.
10. Кинематический анализ выполняют для групп Ассура, в которых неизвестной является кинематика средней кинематической пары.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.