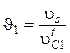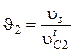Учебное пособие по курсу "Теория механизмов и машин", страница 96

                                    ; .                        (14.60)

За время одного оборота шестерни колесо не совершает полного оборота. Следовательно, его зубья в i₁₂ раз реже вступают в контакт и поэтому меньше изнашиваются. Для сравнения интенсивности износа зубьев по величинам относительных скольжений разделяют J₂ на i₁₂ = z₂/z₁:

                                       .                           (14.61)

Расчетные формулах для J₁ и J₂ имеют вид:

                                      ;                           (14.62)

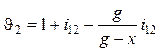                                    .                        (14.63)

В формулах (14.62) и (14.63):

передаточное отношение

i₂₁ = 1/i₁₂ = z₁/z₂;                            (14.64)

g — длина линии зацепления В₁В₂ (см. рис. 14.17, 14.18 и 14. 26);

                                          g = a_w sin a_w;                              (14.65)

х — расстояние, отсчитываемое от точки В₁; х_min = 0; х_max = g.

В соответствии со свойством 4 эвольвенты (п. 14.4) расстояние х равно радиусу кривизны r₁ эвольвенты профиля шестерни в точке контакта. В этом случае радиус кривизны профиля колеса

                                            r₂ = g – r₁.                                (14.66)

На рис. 14.26, а показаны:

– линия зацепления В₁В₂ и активная линия зацепления А₁А₂;

– диаграммы удельных скольжений шестерни J₁ и колеса J₂.

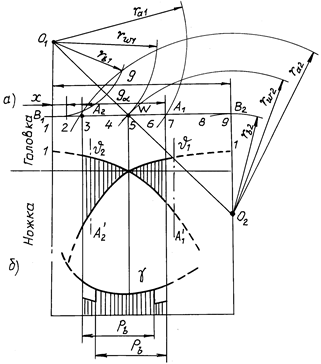
Рис. 14.26

В точках В₁ и В₂ диаграммы имеют ординаты 1 и –¥. Практически диаграммы реальны в пределах активной линии зацепления А₁А₂. За ее пределами диаграммы показаны штриховыми линиями.

NB 14.28. Признаком оптимальной износостойкости является равенство суммарных ординат удельных скольжений в начале и конце зацепления.

На рис. 14.26, а зацепление не будет высокоизносостойким вследствие неравенства суммарных ординат. Удельные скольжения зависят от коэффициентов смещения х₁ и х₂, и их изменением можно достичь оптимальной износостойкости. Так, для достижения равенства суммарных ординат необходимо на линии зацепления переместить активную линию зацепления. На рис. 14.26, а новое положение показано точками  и . Для такого перемещения точек начала и конца зацепления необходимо увеличить диаметр вершин шестерни d_а1 увеличением коэффициента смещения х₁ и уменьшить х₂ и d_a2.

Автором составлена программа ТМ21 в системе GWBASIC для решения задач по оптимизации зацепления по износостойкости с условием вписывания в заданное межосевое расстояние. В компьютерных расчетах задаются смещения х₁ = 0,2 … 1,3 с шагом Dх = 0,1. Коэффициент смещения колеса х₂ = х_S – х₁. Рассчитываются ординаты и суммы ординат удельных скольжений для точек А₂ и А₁ линии зацепления. Анализ распечаток завершается назначением оптимальных коэффициентов смещения.

Пример 14.6. Пользуясь программой ТМ21, рассчитать оптимальные коэффициенты смещения по условиям износостойкости зацепления с m = 10 мм, z₁ = 12, z₂ = 38, а_w = 260 мм.

Решение:

По программе ТМ21 рассчитываем оптимальные коэффициенты смещения. Распечатка компьютерных данных приведена в табл. 14.4.

Таблица 14.4