Учебное пособие по курсу "Теория механизмов и машин", страница 14

NB 4.2. Аналогом ускорения точки называется вторая производная радиуса-вектора точки по обобщенной координате.

Термин «аналог ускорения» был впервые применен Л.В. Ассуром. При равномерном вращении начального звена аналог ускорения

a_q = d²s/dj² = s_j^¢¢ = a/w².                          (4.5)

Аналоги линейных скоростей и ускорений (это скорости и ускорения при w₁ = 1 с^–1 и e₁ = 0) имеют размерность длины (м). При известных аналогах скоростей и ускорений можно найти линейные скорости и ускорения по формулам (4.4) и (4.5).

NB 4.3. Аналогом угловой скорости называется первая производная от угла поворота звена по обобщенной координате.

Он также носит название «передаточное отношение»:

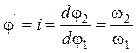                                      .                              (4.6)

4.3. Графические методы. Метод планов

4.3.1. Планы положений механизма

При движении начальных звеньев механизма расположение всех звеньев меняется, но в каждый момент движения оно является вполне определенным.

NB 4.4. Графическое изображение взаимного расположения звеньев, соответствующее выбранному моменту времени, называется планом положений механизма.

Ряд последовательных планов положений, построенных для моментов времени, следующих равномерно друг за другом, позволяет наглядно проследить за движением механизма.

Для определения положений звеньев механизма изображают его кинематическую схему, которую при графическом методе исследования строят в заранее выбранном масштабе. Масштаб плана положений механизма обозначают m_l. Масштаб определяют по правилу, общему для всех масштабов.

NВ 4.5. Масштаб определяют отношением длины отрезка в миллиметрах, изображающего какую-либо физическую величину, к самой физической величине.

Так, для кривошипно-ползунного механизма (рис. 4.1, а) масштаб плана положений в мм/м:

                                          m_l =  / l_AB,                                  (4.7)

где — длина отрезка, мм, изображающего длинукривошипа l_AB, м.

Траектория движения точки B кривошипа - окружность (рис. 4.1, а и 4.2, а). Ее делят на произвольное (например, 12) число равных частей. Тем самым задают изменение угловой координаты j₁ начального звена через каждые 30°.

План положений механизма строят, начиная с нанесения элементов стойки, т.е. неподвижных точек и линий. При выбранном масштабе m_l длины отрезков, которые необходимо отложить на плане положений, получают умножением истинного размера на масштаб. Так, длина отрезка, изображающего длину шатуна:

                                            = l_BC×m_l.                                  (4.8)

NВ 4.6. Для нанесения отрезка на план физическую величину умножают на масштаб.

При заданном положении кривошипа положения остальных звеньев определяют методом засечек. Точку С находят в пересечении дуги радиуса  с направляющей x–x.

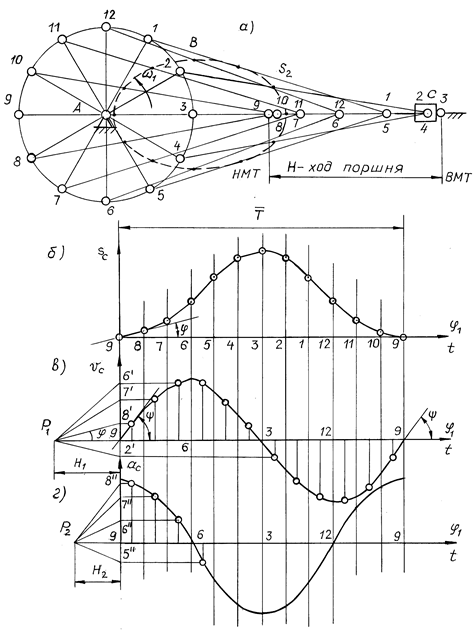
Рис. 4.2

Для построения траектории любой точки механизма строят ряд планов положений механизма и определяют положения заданной точки, например, центра масс S₂ шатуна 2. Для этого от точек B откладывают расстояния BS₂, а плавная кривая, проведенная через все полученные точки, будет искомой траекторией (штриховая линия на рис. 4.2, а). Траектории, описываемые точками шатуна, называются шатунными кривыми.

Траекторией точки С ползуна 3 (рис. 4.2, а) является прямая 9–3, которая представляет собой ход поршня H механизма ДВС или компрессора. Перемещение точки С от нижней мертвой точки определяют расстояниями 9–10, 9–11, 9–12 и т.д.

4.3.2. План скоростей

Так как любой плоский механизм по Ассуру может быть образован из начального механизма I класса, кинематика которого известна, и присоединенных структурных групп Ассура, то, по сути дела, кинематическое исследование такого механизма сводится к исследованию кинематики групп Ассура. При этом в диадах, присоединяемых двумя крайними кинематическими парами к известной кинематической цепи, подлежит определению кинематика средней кинематической пары.

Таким образом, кинематическое исследование механизмов II класса сводится к исследованию одной точки в каждой группе Ассура, в порядке последовательности их присоединения. Это существенно упрощает кинематический анализ диадных механизмов.