Учебное пособие по курсу "Теория механизмов и машин", страница 90

Таблица инволют приведена в прил. Б.

14.12.4. Угол зацепления

В положительном и отрицательном зацеплениях начальные и делительные диаметры не совпадают. Угол профиля по начальной окружности равен углу зацепления a_w. Передачу выполняют так, чтобы между зубьями не оставалось бокового зазора. Так как начальные окружности катятся друг по другу без скольжения, то для беззазорного зацепления необходимо, чтобы начальная толщина зуба одного колеса s_w1 в точности равнялась ширине впадины второго колеса e_w2, то есть s_w1 = e_w2. Аналогично s_w2 = e_w1. Толщина зуба и ширина впадины в сумме равны шагу. Начальный шаг колес

p_w = s_w1 +e_w1 = s_w1 + s_w2.                      (14.42)

Начальный шаг находят из формулы (14.38):

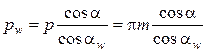                               .                   (14.43)

После подстановки в формулу (14.42) значений из формул (14.40) и (14.43) записывают:

                .              

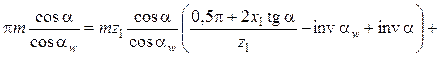
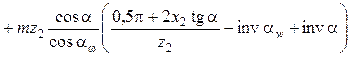После сокращения обеих частей уравнения на 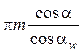 получают:

                                       в окончательном виде:

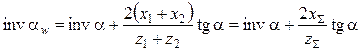               .    (14.44)

NB 14.19. С увеличением положительного смещения угол зацепления увеличивается. В положительном зацеплении он больше угла профиля (>20°).

Угол зацепления находят из таблицы инволют (см. прил. Б). Существуют и другие методы (см. пп. 14.12.5).

14.12.5. Геометрические параметры зацепления

На рис. 14.18 представлено внешнее положительное эвольвентное зацепление. Один из важнейших параметров зацепления — делительное межосевое расстояние, которое рассчитывают по формуле (14.29). Оно не зависит от смещения и остается неизменным. Межосевое расстояние a_w зависит от величин смещений колес и соответствует выражению

                                           a_w = a + ym,                               (14.45)

где y — коэффициент воспринимаемого смещения.

Как было отмечено ранее, в положительных колесах увеличиваются диаметры вершин и впадин, в результате они не смогут вписаться в делительное межосевое расстояние. Оси колес в первом приближении следует раздвинуть на сумму смещений x_S = m(x₁ + + x₂). Радиальный зазор при этом остается стандартным (0,25 m). Однако при этом между нерабочими поверхностями зубьев возникнет недопустимо большой боковой зазор. При изменении направления вращения колес (реверсе) могут возникнуть дополнительные динамические нагрузки.

Проблема решается, если спроектировать передачу с последующим сдвигом колес навстречу друг другу на величину Dym, где Dy — коэффициент уравнительного смещения. Образуется зацепление с нормированным боковым зазором j_n, но для обеспечения стандартного радиального зазора зубья колес необходимо «обрезать» на величину Dym. Из приведенных рассуждений следует, что коэффициент воспринимаемого смещения равен:

                                 y = x₁ + x₂ – Dy = – Dy.                     (14.46)

Высота зуба при этом уменьшается на величину уравнительного смещения:

                                       h = m (2,25 – Dy).                           (14.47)

Межосевое расстояние можно также рассчитать как полусумму начальных диаметров колес. Их размеры рассчитывают из формулы (14.35):

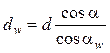                                         .                             (14.48)

Межосевое расстояние

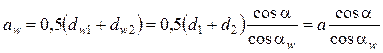             .  (14.49)

Из формулы (14.49) можно определить угол зацепления при известных прочих параметрах:

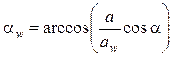                                  .                       (14.50)

Начальные диаметры при известном межосевом расстоянии могут быть рассчитаны по формулам:

d_w2 = i₁₂d_w1;                               (14.51)

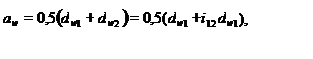                                         откуда

d_w1 = 2a_w/(i₁₂ + 1).                           (14.52)

Диаметры вершин с учетом (14.21) рассчитывают по формуле

                                 d_a = m (z + 2 + 2x – 2Dy).                     (14.53)

Диаметры впадин:

                                     d_f = m (z – 2,5 + 2x).                         (14.54)