Учебное пособие по курсу "Теория механизмов и машин", страница 7

На плоскости одноподвижные пары являются низшими, так как звенья в них соприкасаются по цилиндрической поверхности или по плоскости, двухподвижные пары — высшими (элементы зубчатых или кулачковых механизмов). Таким образом, в формуле Чебышева:

p₁ — число низших кинематических пар;

p₂ — число высших кинематических пар.

Пример 3.2. Рассчитать число степеней свободы рычажного механизма двигателя внутреннего сгорания (рис. 3.2).

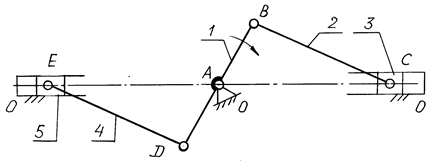
Рис. 3.2

Решение:

Выполним построения и обозначения в соответствии с примером 3.1. Заданная кинематическая цепь — плоская замкнутая. Составляем таблицу пар и звеньев (табл. 3.2).

Таблица 3.2

Число подвижных звеньев n = 5, число низших кинематических пар (равно числу строк в таблице) p₁ = 7, высших пар нет (p₂ =  = 0). Число степеней свободы W = 3×5 – 2×7 – 0 = 1. Это означает, что механизм имеет одну обобщенную координату (угловую j или линейную x), которая задается одному звену, называемому начальным. Это может быть входное звено либо выходное. Таким в механизме ДВС является кривошип 1, конструктивно выполняемый в виде коленчатого вала. Ему задается угловая координата j.

3.3. Избыточные связи и лишние степени свободы

В некоторых плоских механизмах имеются особенности, которые могут быть учтены видоизмененной формулой Чебышева:

W = 3n – 2p₁ – p₂ + q_п,                           (3.3)

где q_п – число пассивных (избыточных) связей.

Избыточные связи иногда умышленно вводят в состав механизма для повышения прочности или жесткости звеньев. Так, в механизме сдвоенного параллелограмма (рис. 3.3) приняты соотношения: AB = CD и BC = AD (т.е. фигура ABCD — параллелограмм), AE = FD (т.е. фигура AEFD — тоже параллелограмм). По свойству параллелограмма расстояния между точками E и F всегда равны отрезку AD, если эти точки находятся на равных расстояниях от точек A и D. Поэтому введение дополнительного звена 4 при условии EF = AD не вносит новых геометрических связей.

Рассматриваемый механизм является механизмом с одной избыточной связью. Его число степеней свободы по формуле Чебышева W = 3×4 – 2×6 = 0, хотя не вызывает сомнений, что ABCDEF не ферма, а механизм. По формуле (3.3) W = 3×4 – 2×6 + 1 = 1. Такой же результат получается из формулы (3.2) после удаления звена 4: W = 3×3 – 2×4 = 1. В общем случае в отличие от рассмотренного избыточные связи можно выявить только при кинематическом исследовании механизма. В дальнейшем будут рассматриваться механизмы без избыточных связей с q_п = 0.

Характерным примером механизма с лишней степенью свободы является кулачковый механизм (рис. 3.4). Его число степеней свободы W = 3×3 – 2×3 – 1 = 2, что говорит о двух начальных звеньях. Однако единственно возможное движение ведущего звена — вращение кулачка; вторая степень свободы связана с вращением ролика относительно собственной оси, не оказывающим влияния на кинематику. Ролик создает лишнюю степень свободы, и перед структурным анализом его необходимо удалить. В данном механизме лишнюю степень свободы вводят для повышения коэффициента полезного действия (замена трения скольжения трением качения), а также для уменьшения и выравнивания износа в высшей кинематической паре. После удаления ролика W = 3×2 – 2×2 – 1 = 1.

NB 3.2. Перед структурным анализом ролик толкателя удаляют, а кулачок эквидистантно увеличивают на радиус ролика.

3.4. Группы Ассура