Учебное пособие по курсу "Теория механизмов и машин", страница 114

                                             r_р £ 0,4r₀.                                 (16.25)

16.8.2. Аналитический метод

Для профилирования кулачка определяют зависимость радиуса-вектора центрового профиля кулачка в функции от обобщенной координаты. Координату нижнего положения толкателя определяют через радиус начальной окружности и смещение:

                                         .                             (16.26)

Текущий радиус-вектор в фазе удаления определяют по рис. 16.11:

                                    .                         (16.27)

При профилировании кулачка задают полярную ось, от которой отсчитывают углы a_i, соответствующие определенным углам поворота кулачка φ_i, и рассчитывают радиусы-векторы r_i. Углы a_i откладывают по методу обращения движения в направлении против вращения кулачка.

Во внецентренном кулачковом механизме с поступательно движущимся толкателем углы профиля кулачка a_i не равны соответствующим углам поворота кулачка φ_i. В начале фазы удаления (рис. 16.13) контакт кулачка и толкателя происходит в точке а. Для произвольной точки кулачка b радиус-вектор r_i = Оb составляет с радиусом-вектором точки а (r₀ = Оа) угол a_i. При повороте кулачка в направлении w₁ на угол φ_i до контакта точки b с толкателем она займет положение . Точка находится на пересечении дуги окружности радиуса r_i с траекторией движения толкателя а.

Для того, чтобы точка контакта переместилась из точки a в точку b, необходимо кулачок повернуть на угол φ_i, отличающийся от угла a_i на величину D_i = d_i – d₀; соответствующие углы профиля определяются по формулам:

                                       a_i = φ_i – (d_i – d₀);                                     

                                        d_i = arccos (e/r_i);                            (16.28)

                                       d₀ = arccos (e/r₀).                                     

Величины S_i, соответствующие углам поворота кулачка φ_i, рассчитаны предварительно по аналитическим зависимостям. Табличная функция r_i = r_i(a_i) определяет центровой профиль кулачка.

С использованием полярной системы координат легко строится соответствующий центровой профиль. В соответствии с методом обращения движения углы откладывают от оси x в направлении, противоположном вращению кулачка. Для определения и построения конструктивного профиля используют векторное соотношение (рис. 16.14):

                                            .                                (16.29)

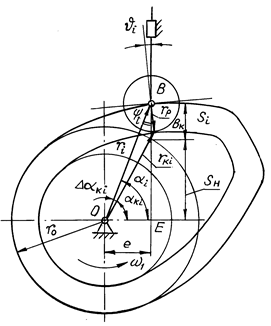
Рис. 16.14

Радиус-вектор ролика  всегда располагается по нормали к профилю и отклоняется от вертикали на угол давления J. Радиус-вектор центрового профиля расположен к вертикали под углом y_i. Сумма названных углов является углом между векторами  и . Угол y_i находят из прямоугольного треугольника ОВЕ:

                     или 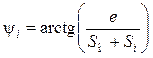.        (16.30)

Модуль радиуса-вектора конструктивного профиля определяют из треугольника ОВВ_к по теореме косинусов:

                            .                (16.31)

Угол отклонения радиуса-вектора конструктивного профиля от радиуса-вектора центрового профиля определяют с помощью теоремы синусов из векторного треугольника ОВВ_к:

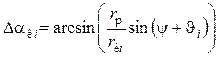                              .                  (16.32)

Угол радиуса-вектора конструктивного профиля

                                        .                            (16.33)

Угол давления J — величина переменная, его определяют по формуле:

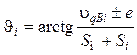                                      ,                          (16.34)

где знак «минус» ставят для фазы удаления, «плюс» — для фазы сближения.

Пример 16.2. По исходным данным примера 16.1 рассчитать радиусы-векторы центрового профиля r_i, a_i и конструктивного профиля r_кi, a_кi.

Решение:

В системе MathCAD по программе ТММ-17 рассчитываем искомые параметры. Копии таблицы и графика r_кi = r_кi (a_кi) приведены на рис. 16.15, профили кулачка — на рис. 16.16.

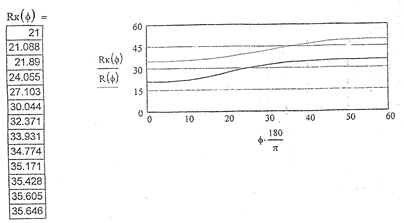
Рис. 16.15

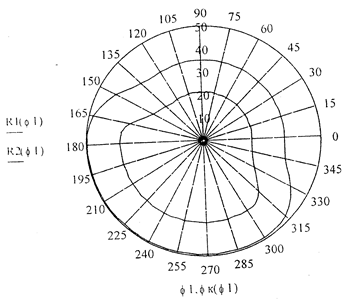
Рис. 16.16