Машиностроение \ Теории механизмов и машин

Учебное пособие по курсу "Теория механизмов и машин", страница 59

5. Выполняем аналитическим методом расчеты на ПЭВМ по программе TMM-12-8, составленной в среде Quick BASIC. При разработке алгоритма расчета использовался векторный метод. Исходные векторы ,и  рассчитывались из уравнений проекций выражений (9.13), (9.16) и (9.17) на координатные оси. Результаты компьютерных расчетов:

                m1 = 40 г; r2 = 80 мм; j1 = 253о; D1 = 3200 г×мм;              

                m5 = 40 г; r5 = 44 мм; j5 = 316о; D5 = 1760 г×мм;              

               = 40 г;  = 72 мм;  = 220о;  = 2880 г×мм.            

Вывод:

Результаты графического и аналитического методов практически совпадают. Максимальная погрешность угла j составляет 5º (2,3%), дисбаланса D — 2,4 %.

Лекция № 13

9.7. Балансировка ротора с неизвестным дисбалансом

Изложенный в п. 9.4–9.6 метод балансировки ротора с известными дисбалансами достаточно нагляден и эффективен в учебных целях. Однако на практике случаи, когда известны величины и положения неуравновешенных масс, встречаются редко. Кроме того, на точность балансировки влияет неоднородность материала, погрешности изготовления и другие факторы. Поэтому быстроходные роторы подвергают динамической балансировке на специальных станках.

Неуравновешенный ротор 1 (рис. 9.5) устанавливают в балансировочном станке. На роторе специально сконструированы два симметрично расположенных диска — A и B. Ротор устанавливают в подшипники 2 маятниковой рамы 3. Подвес рамы подпружинен и может совершать колебания в вертикальной плоскости относительно оси 4. Амплитуду колебаний рамы измеряют индикатором часового типа 5.

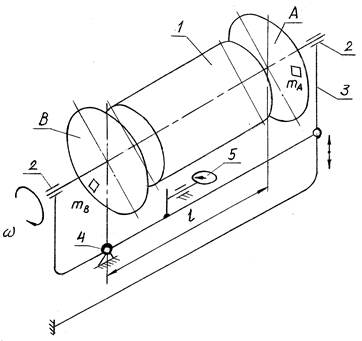
Рис. 9.5

Рис. 9.6

Динамическая неуравновешенность ротора может быть устранена с помощью двух корректирующих масс, устанавливаемых на дисках A и B. Диск B располагают в плоскости, проходящей через ось качания 4 рамы 5. В этом случае вектор дисбаланса DB не создает момента относительно оси 4 и на вынужденные колебания системы ротор-рама влияния не оказывает. При вращении ротора вертикальная составляющая дисбаланса DA создает относительно оси 4 момент дисбаланса (рис. 9.6):

                                      ,                            (9.18)

где l — расстояние между дисками.

Момент , изменяющийся по гармоническому закону с частотой , равной угловой скорости ротора, вызовет вынужденные колебания рамы с установленным на ней ротором. При свободном выбеге частота  будет убывать и когда она станет равной частоте собственных колебаний рамы, возникает резонанс. Максимальную амплитуду резонансных колебаний фиксируют индикатором 5.

Из теории колебаний известно, что амплитуда вынужденных колебаний пропорциональна амплитуде возмущающего фактора:

                       .             (9.19)

При резонансе амплитуда вынужденных колебаний пропорциональна дисбалансу:

                                      ,                           (9.20)

где  — максимальная амплитуда колебаний системы, вызванная силами инерции от неуравновешенной массы, мм;  — коэффициент пропорциональности, зависящий от параметров станка, мм/(г×мм);  — среднее арифметическое абсолютных значений дисбаланса, г×мм,

                                            .                                          

Для определения коэффициента  и параметров корректирующих масс на балансируемой детали на диске A устанавливают дополнительную массу , дисбаланс которой равен:

.

Для определения величины начального дисбаланса в плоскости диска 3 применяют способ трех пусков. При первом пуске (рис. 9.7, а) определяют максимальную амплитуду  колебаний рамы, вызванных дисбалансом  от неуравновешенной приведенной массы в плоскости диска A. При втором пуске (рис. 9.7, б) определяют амплитуду колебаний рамы, вызванных неуравновешенной приведенной массой  и дополнительной массой , которую устанавливают в произвольном положении. Амплитуду колебаний ротора с дополнительной массой определяют по равенству

                                                                        (9.21)

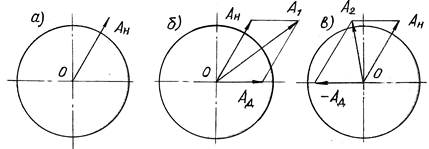
Рис. 9.7

Скачать файл