Эффект внутреннего зацепления наиболее ярко
проявляется при малой разнице чисел зубьев центральных колес z1
и z3 и сателлитов соответственно
z2 и ![]() . Это реализовано в конструкции
класса 2k – h на рис. 13.4. Такая схема не позволяет установить
более одного сателлита и требует установки противовесов. Интервалы передаточных
отношений
. Это реализовано в конструкции
класса 2k – h на рис. 13.4. Такая схема не позволяет установить
более одного сателлита и требует установки противовесов. Интервалы передаточных
отношений ![]() = 25 …
300 при КПД
= 25 …
300 при КПД ![]() = 0,9 … 0,4.
= 0,9 … 0,4.
|
|
|
|
Рис. 13.3 |
Рис. 13.4 |
|
Рис. 13.5 |
В силовых передачах применяют модификацию смешанного вида с внешним и внутренним зацеплениями (эпигипоциклический механизм, рис. 13.5). Его передаточное отношение всегда положительно. Это следует из формулы:
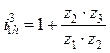 . (13.13)
. (13.13)
Такой механизм имеет высокий КПД и достаточно
широко применяется в силовых механизмах. Он имеет передаточные отношения ![]() = 7…16 и высокий КПД (до 0,97), но уступает
редуктору Джеймса в простоте конструкции и габаритах. Отличительной особенностью
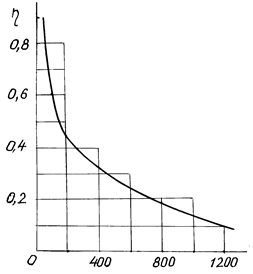
планетарных механизмов различных схем является значительное уменьшение КПД с
ростом передаточного отношения (рис. 13.6).
= 7…16 и высокий КПД (до 0,97), но уступает
редуктору Джеймса в простоте конструкции и габаритах. Отличительной особенностью
планетарных механизмов различных схем является значительное уменьшение КПД с
ростом передаточного отношения (рис. 13.6).
 i
i
Рис. 13.6
А) В механизмах класса 3k (рис. 13.7) основными звеньями являются три центральных колеса — 1, 3 и 4. Водило h не является основным звеном и представляет собой конструктивный элемент для поддержания осей сателлитов. Передаточное отношение механизма может быть рассчитано после его разделения на две части:
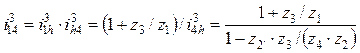 . (13.14)
. (13.14)
Механизм класса 3k с двухвенцовым
сателлитом работает в интервале передаточных отношений ![]() =
20…500 с
=
20…500 с ![]() = 0,9…0,8.
= 0,9…0,8.
Б) Механизм класса k – h – u (рис. 13.8) состоит из одного центрального колеса 1 с внутренними зубьями (k), водила h и соосного с ним звена u. Специальное устройство с передаточным отношением, равным единице, и называемое механизмом w, передает момент с сателлита 2 звену u. Механизм является аналогом волновой зубчатой передачи.
|
|
|
|
Рис. 13.7 |
Рис. 13.8 |
Если в редукторе Джеймса раскрепить колесо 3, то такой механизм станет дифференциальным (дифференциалом, рис. 13.9). Число степеней свободы
W = 3×4 – 2×4 – 2 = 2.
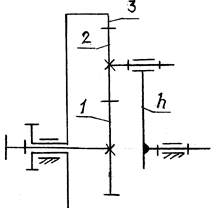
Рис. 13.9
Таким образом, для определенности движения механизм должен иметь заданными законы движения двух звеньев. Например, звеньев 1 и 3, 1 и h или 3 и h.
NB 13.4. Дифференциалом называется зубчатый механизм с подвижными осями, в котором все колеса вращаются.
Если задаться законами движения углов поворота колес 1 и 3, то угол поворота ведомого водила h может быть записан формулой общего вида:
![]() .
.
По правилу дифференцирования сложных функций выводят уравнение дифференциалов:
![]() .
(13.15)
.
(13.15)
NB 13.5. Угловая скорость ведомого звена дифференциала равна сумме угловых скоростей ведущих звеньев. Каждое слагаемое умножается на постоянный численный коэффициент, равный передаточному отношению от ведомого звена к ведущему при остановленном втором ведущем.
Если в дифференциале ведущие звенья соединить между собой дополнительной зубчатой передачей, то образуется замкнутый дифференциальный механизм (рис. 13.10). Число степеней свободы
W = 3×6 – 2×6 – 5 = 1.
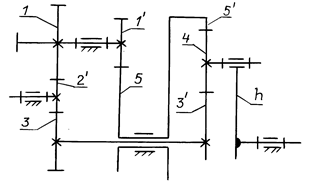
Рис. 13.10
Такой механизм требует задания одной обобщенной
координаты, т.е. одного ведущего звена. В данном механизме ведущим является
звено 1, которое через дополнительную кинематическую цепь z1/![]() /z3 –
/z3 – ![]() /z5 передает
вращательное движение на ведущие колеса дифференциала
/z5 передает
вращательное движение на ведущие колеса дифференциала ![]() и
5. Водило h — ведомое звено.
и
5. Водило h — ведомое звено.
NB 13.6. В замкнутом дифференциальном механизме оба ведущих звена связаны дополнительной кинематической цепью, уменьшающей число степеней свободы механизма до единицы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.