Учебное пособие по курсу "Теория механизмов и машин", страница 11

NВ 3.12. Порядок замены высших пар низшими:

1)  в точке контакта двух соприкасающихся профилей высшей кинематической пары проводят общую нормаль;

2)  на нормали находят центры кривизны и в них ставят низшие пары;

3)  дополнительные низшие пары соединяют звеном друг с другом и с ближайшими заданными низшими парами.

Если центры кривизны соприкасающихся профилей постоянные, то заменяющий механизм эквивалентен заданному во всех положениях, как, например, в механизме зубчатой пары (рис. 3.20). В противном случае заменяющий механизм эквивалентен заданному только в определенном положении (рис. 3.19, 3.21, 3.22).

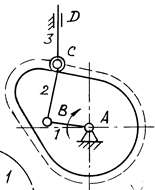
Если центр кривизны элемента высшей пары лежит в бесконечности, вместо вращательной пары ставится поступательная пара (рис. 3.21, а). Если же радиус кривизны равен нулю, как, например, в точке касания элементов кулачкового механизма, то шарнир ставится в этой точке (рис. 3.21, б). Следует помнить, что в кулачковом механизме перед заменой высшей пары низшими необходимо ролик удалить (рис. 3.22).

Рис. 3.21	Рис. 3.22

Пример 3.4. Выполнить структурный анализ суммирующего механизма (рис. 3.23).

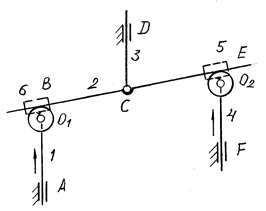
Рис. 3.23

Решение:

Вычерчиваем кинематическую схему. Составляем таблицу звеньев и пар (табл. 3.6).

Таблица 3.6

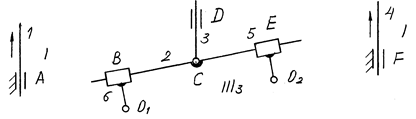
Рис. 3.24

Число звеньев n = 4, число низших (одноподвижных) пар p₁ = 4, число высших пар p₂ = 2. Число степеней свободы W = 3×4 – 2×4 – – 2 = 2. Заменяем высшие пары низшими. Для этого в точках B и E (рис. 3.23) ставим ползуны, в центрах кривизны O₁ и O₂ цилиндров — шарниры, которые соединяем с ползунами. Образовавшиеся при этом звенья 5 и 6 содержат по одной вращательной и одной поступательной паре. Составляем таблицу звеньев и пар заменяющего механизма (табл. 3.7).

Таблица 3.7

В заменяющем механизме n = 6 и p₁ = 8. Число степеней свободы W = 3×6 – 2×8 = 2. Структурная эквивалентность соблюдается. Начинаем отсоединение с наиболее удаленного звена CD. Кинематическая цепь, состоящая из звеньев 2 и 3, не является группой Ассура, так как включает не 3, а 4 кинематические пары (B, C, D, E). Поэтому отсоединяем группу Ассура более высокого класса, состоящую из четырех звеньев (2, 3, 5, 6) и шести пар (рис. 3.24). Данная группа Ассура относится к III классу (звено 2 входит в три пары — B, C и E) и 3-му порядку (свободные пары O₁, O₂ и D). Остаются два начальных механизма I класса. Формула строения заменяющего механизма

                                I(1) – III₃(5, 2, 3, 6) – I(4).                              

Механизм относится к III классу.

Пример 3.5. Выполнить структурный анализ механизма указателя вертикальной скорости самолета (рис. 3. 25).

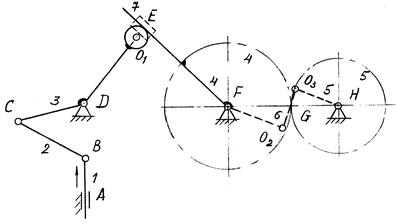
Рис. 3.25

Решение:

Вычерчиваем кинематическую схему. Таблицу звеньев и пар в примере опускаем. Число звеньев механизма n = 5, число низших пар p₁ = 6 (A, B, C, D, F, H), число высших пар p₂ = 2 (E, G). Число степеней свободы W = 3×5 – 2×6 – 2 = 1.