Эвольвента окружности есть кривая, центры кривизны которой лежат на окружности. Эвольвента (в переводе «развертка») может быть получена как траектория любой точки прямой, перекатывающейся без скольжения по окружности.
NB 14.3. Эвольвенту описывает каждая точка прямой, катящейся без скольжения по окружности.
Окружность, являющаяся геометрическим местом кривизны эвольвенты, называется эволютой. Она служит для образования эвольвенты. В теории зацепления окружность, эвольвентой которой является профиль зуба, называется основной окружностью.
NB 14.4. Основной называется окружность, служащая для образования эвольвенты.
Этапы вычерчивания эвольвенты показаны на рис. 14.2. Начальная точка эвольвенты обозначена М0. Путем перекатывания прямой по основной окружности в направлении по часовой стрелке по четырем точкам строят правую ветвь эвольвенты.
|
Рис. 14.2 |
Прямая МоМn называется производящей прямой, точка Мо — производящей точкой. Окружность радиуса rb (b — basis — основа) — основная окружность. Из условия перекатывания без скольжения записывают равенства прямых и дуг окружностей при касании производящей прямой с основной окружностью в точках М1, М2 и М3:
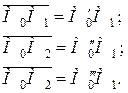(14.9)
Острый угол
между касательной к эвольвенте в точке 
и
радиусом-вектором эвольвенты 
обозначают через a. В теории эвольвентного зацепления он называется
углом профиля.
NB 14.5. Острый угол a между касательной к эвольвенте и радиусом-вектором, проведенным через точку касания, называется углом профиля.
NB 14.6. Угол, образованный начальным радиусом-вектором
эвольвенты и ее текущим радиусом-вектором, называется эвольвентным углом и
обозначается 
.
Используя уравнение (14.9), записывают:
rbtga = rb( + a), откуда
= tga
– a. (14.10)
Тригонометрическая функция tga – a называется инволютой (эвольвентной функцией) и обозначается inv a. Таблица инволют приведена в прил. Б. Таким образом, эвольвентный угол равен инволюте угла профиля:
=
inv a. (14.11)
Радиус-вектор
эвольвенты находят из 
:
r = rb/cos a. (14.12)
Формулы (14.11) и (14.12) определяют уравнение
эвольвенты в полярных координатах r и .
Текущие значения a, и r снабжают
индексом y: ay, y, ry.
Вторую ветвь эвольвенты (на рис. 14.2 показана штриховой линией) образуют перекатыванием
производящей прямой МоМn в направлении
против часовой стрелки.
Свойства эвольвенты:
1. Каждая из двух ветвей эвольвенты вполне определяется радиусом основной окружности и положением начала отсчета эвольвентного угла.
2. Эвольвента не имеет точек внутри основной окружности.
3. Нормаль к любой точке эвольвенты направлена по касательной к основной окружности. Это свойство используется для измерения одного из контрольных параметров — длины общей нормали W (рассматривается в п. 14.17).
|
Рис. 14.3 |
4. Центр кривизны эвольвенты лежит в точке касания нормали с основной окружностью. Это следует из определения основной окружности как геометрического места центров кривизны эвольвенты. Данное свойство позволяет определить радиус кривизны эвольвенты в любой ее точке как расстояние от точки на эвольвенте до точки касания нормали с основной окружностью (см. рис. 14.2):
. (14.13)
5. Если основной радиус равен бесконечности (т.е. эволюта превращается в прямую), то эвольвента преобразуется также в прямую, перпендикулярную к эволюте (рис. 14.3), а зубчатое колесо превращается в зубчатую рейку.
Пример 14.1. Рассчитать параметры y, ry
и 
и построить правую ветвь эвольвенты, если
задан основной радиус rb = 60 мм.
Решение:
Задаем последовательно углы профиля 
= 0 … 66º (в табл. 14.1 вносим значения,
позволяющие получить точки эвольвенты на приблизительно равных расстояниях друг
от друга). Эвольвентный угол в радианах находим из прил. В и переводим в градусы.
Текущий радиус-вектор ry находим по формуле (14.12), радиус кривизны — по формуле (14.13). Данные расчетов
сводим в табл. 14.1.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
