Выполняем замену высших пар низшими. В центрах кривизны O1, O2 и O3 ставим шарниры. В точке Е ставим ползун и соединяем его с шарниром O1, шарниры O2 и O3 соединяем друг с другом дополнительным звеном 6, с шарниром Н — звеном 5 и с шарниром F — элементом звена 4. Заменяющий механизм на рис. 3.25 строим сплошными основными и штрихпунктирными линиями. Его число степеней свободы W = 3×7 – 2×10 = 1. Структурная эквивалентность выполняется.
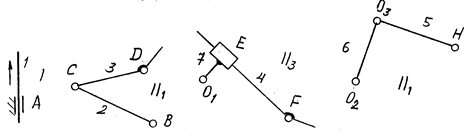
Рис. 3.26
Отсоединяем последовательно вначале наиболее удаленную диаду O2O3H (1-го вида, рис. 3.26), затем диады O1EF (3-го вида) и BCD (1-го вида). Остается начальный механизм I класса. Формула строения:
I(1) – II1(2, 3) – II3(7, 4) – II1(6, 5).
Механизм относится ко II классу.
1. Обобщенная координата механизма — угловой или линейный параметр начального звена.
2. Число степеней свободы механизма — число обобщенных координат, равное числу начальных звеньев.
3. Формула Малышева — структурная формула пространственной кинематической цепи для определения числа степеней свободы.
4. Формула Чебышева — структурная формула плоской кинематической цепи.
5. Перед структурным анализом ролик толкателя кулачкового механизма удаляют, а кулачок эквидистантно увеличивают на радиус ролика.
6. Группа Ассура — плоская кинематическая цепь, содержащая низшие пары, с числом степеней свободы, равным нулю.
7. Класс группы Ассура определяется числом кинематических пар, входящих в наиболее сложный контур.
8. Порядок группы Ассура определяется числом внешних (потенциальных) кинематических пар.
9. Диада — двухповодковая группа Ассура, состоящая из двух звеньев и трех кинематических пар.
10. Диадный механизм — механизм, составленный из диад.
11. Базовая диада содержит три вращательные пары; диады других видов образуются путем замены в базовой диаде одной или двух вращательных пар поступательными.
12. Начальный механизм I класса — кинематическая цепь, состоящая из подвижного звена (кривошипа или ползуна), стойки и низшей пары.
13. Структурный синтез рычажных механизмов (проектирование схемы) заключается в присоединении к начальному механизму I класса групп Ассура.
14. Рычажный механизм — плоский механизм с одноподвижными кинематическими парами.
15. Структурный анализ заключается в отсоединении групп Ассура по заданной схеме механизма.
16. Класс механизма определяется по той группе Ассура, которая относится к наивысшему классу.
17. Высшая кинематическая пара заменяется кинематической цепью, состоящей из одного звена и двух низших пар.
W — число степеней свободы механизма;
n — число подвижных звеньев;
p1, p2, …p5 — число одноподвижных, двух-, … пятиподвижных кинематических пар;
qп — число пассивных (избыточных) связей.
1. Вывод формул Малышева и Чебышева.
2. Структурные группы Ассура. Классификация групп Ассура и механизмов.
3. Структурный синтез механизмов по Ассуру. Образование рычажных механизмов.
4. Избыточные связи и лишние степени свободы.
5. Замена высших кинематических пар низшими.
А. Задачи № 1, 2, 3, 4 (рис. 3.27, а, б … 3.30, а, б) [9]
Определить число степеней свободы механизма с гидроцилиндрами и «руки» манипулятора (кинематическую пару захвата не учитывать).
а)
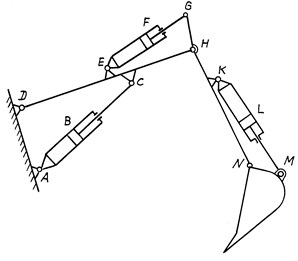
б)
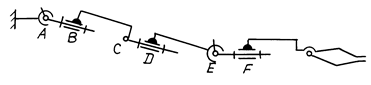
Рис. 3.27
а)
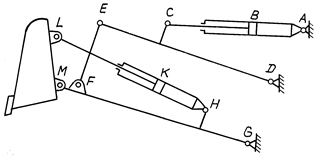
б)
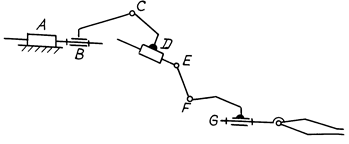
Рис. 3.28
а)
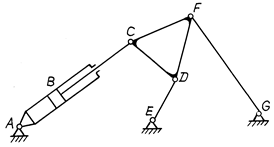
б)
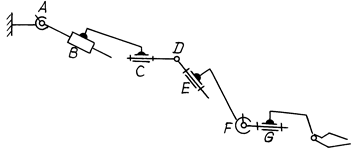
Рис. 3.29
а)
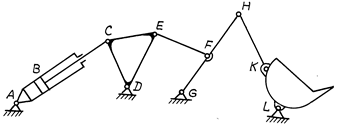
б)
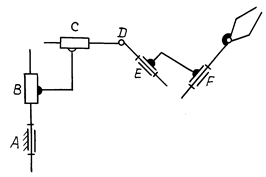
Рис. 3.30
Б. Задачи № 5, 6, 7, 8 (рис. 3.31–3.34) [9]
Выполнить структурный анализ рычажного восьмизвенника: определить число степеней свободы, отсоединить группы Ассура и записать формулу строения механизма.
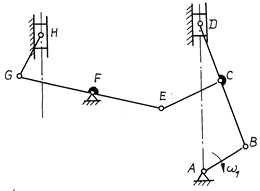
Рис. 3.31
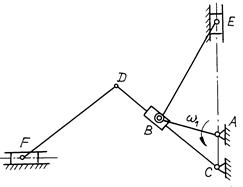
Рис. 3.32
|
|
|
|
Рис. 3.33 |
Рис. 3.34 |
В. Задачи № 9, 10, 11, 12, 13, 14, 16 (рис. 3.35–3.41) [9]
Выполнить структурный анализ механизма с высшими кинематическими парами: определить число степеней свободы, заменить высшие пары низшими, отсоединить группы Ассура и записать формулу строения механизма.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.