Учебное пособие по курсу "Теория механизмов и машин", страница 81

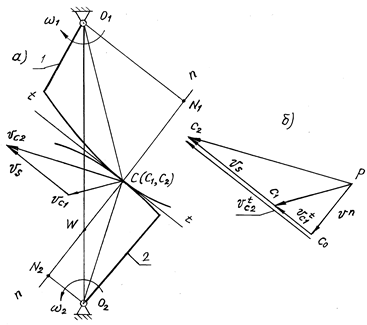
Рис. 14.1

Выполняют дополнительные построения. Из полюса плана скоростей р опускают перпендикуляр рс₀ на направление t–t. Абсолютные скорости точек С₁ и С₂ могут быть разложены по направлениям n–n и t–t и представлены векторным равенством

                                          .                                (14.3)

Нормальные составляющие υⁿ являются общими для скоростей _С1 и _С2. В противном случае профили теряли бы контакт и не были сопряженными. Касательные составляющие абсолютных скоростей:

                                   ; .                         (14.4)

Переносят векторы из плана скоростей в точку контакта С. Векторы абсолютных скоростей _С1 и _С2, как и следует из построений плана скоростей, перпендикулярны соответствующим радиусам О₁С₁ и О₂С₂. Вектор _С2С1 направлен по общей касательной t–t и является скоростью скольжения _s.

Из точек О₁ и О₂ опускают перпендикуляры ON₁ и ON₂ на нормаль n–n. Из построений видно:

           подобен ;  подобен .         

Из подобия треугольников находят пропорции:

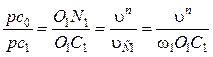                              ;                    (14.5)

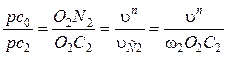                             .                   (14.6)

Из пропорций (14.5) и (14.6) находят ⁿ:

                                  ,                                 откуда

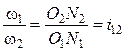                                       .                            (14.7)

Треугольники O₁N₁W и O₂N₂W также подобны. Из их подобия составляют пропорцию:

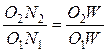                                                                                 и с учетом (14.7)

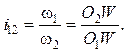                                                                    (14.8)

Пропорция (14.8) называется основной теоремой зацепления.

NB 14.1. Нормаль в точке соприкасания элементов высшей пары качения и скольжения делит межосевую линию на части, обратно пропорциональные угловым скоростям.

Из формулы (14.8) видно, что при изменении передаточного отношения i₁₂ изменяются длины О₁W и О₂W и точка W будет занимать разные положения на линии центров О₁О₂. Отсюда — важнейшее следствие:

NB 14.2. Для того, чтобы передаточное отношение было постоянным, общая нормаль к профилям в точке соприкасания должна пересекать межосевую линию в одной и той же точке, называемой полюсом зацепления.

Итак, для обеспечения основной теоремы зацепления необходимо, чтобы полюс W на межосевой линии не изменял своего положения. По той же причине желательно, чтобы нормаль n-n также не изменяла своего положения.

Таким образом, геометрия сопряженных профилей должна удовлетворять основной теореме зацепления.

При выборе формы профиля зуба на практике также приходится руководствоваться соображениями кинематического, динамического, технологического и эксплуатационного характера.

Соображения кинематического характера заключаются в требовании, чтобы профили могли быть построены достаточно простыми геометрическими приемами.

Соображения динамического характера заключаются во многих требованиях, основные из них:

– при постоянной мощности давления на зубья и опоры должны быть постоянными;

– зубья должны иметь форму, обеспечивающую наибольшую прочность и износостойкость.

Требования технологического характера заключаются в проектировании профилей, которые могли бы быть достаточно просто изготовлены на современных станках.

Требования эксплуатационного характера заключаются в проектировании профилей, которые обеспечивают долговечность механизма, безударность и бесшумность работы, простоту замены (условие взаимозаменяемости).

Поэтому, хотя теоретически можно спроектировать зубчатый механизм с самыми различными профилями зубьев, удовлетворяющими основной теореме зацепления, практически выбор очертания профилей в значительной степени стеснен вышеизложенными требованиями. Вследствие этого в машиностроении пользуются только несколькими видами кривых в качестве профилей зубьев: эвольвента, циклоида, дуга окружности (последняя только в косозубом зацеплении).

14.4. Эвольвента окружности

Большинство современных зубчатых колес имеют эвольвентные профили. Эвольвентное зацепление было предложено петербургским академиком Л. Эйлером в 1761 г.