Нулевой будет передача, составленная из нулевых колес. Также нулевой будет равносмещенная передача, в которой положительное смещение одного колеса равно по абсолютной величине отрицательному смещению другого колеса:
х2 = –х1.
В обоих вариантах нулевых передач коэффициент
суммы смещений 
= 0 ( =
x1 + x2). Следует помнить, что меньшее из
двух колес зацепления называется шестерней, большее — колесом.
NB 14.13. Нулевая передача может быть составлена либо из нулевых колес, либо из положительной шестерни и отрицательного колеса с равными по модулю смещениями.
2) В
положительной передаче делительные и начальные окружности не совпадают, а
коэффициент суммы смещений > 0. Положительная
передача может быть образована:
– двумя положительными колесами;
– нулевым и положительным колесами;
– положительным и отрицательным колесами.
Чаще всего она образуется положительными колесами. В положительном зацеплении межосевое расстояние aw больше, чем в нулевом, так как диаметры вершин колес увеличиваются, и передачу невозможно вписать в делительное межосевое расстояние a. При увеличении межосевого расстояния увеличивается и угол зацепления, так как основные диаметры не изменяются, а угол зацепления определяется положением общей касательной к обеим основным окружностям.
NB 14.14. В положительной передаче по сравнению с нулевой увеличиваются межосевое расстояние аw и угол зацепления aw. Такая передача чаще всего составляется из положительных колес.
3) В отрицательной передаче хS < 0, аw < а, aw < a. Ее геометрия изменяется по сравнению с положительной передачей в противоположную сторону.
При любом смещении неизменными в зацеплении остаются:
– делительное межосевое расстояние — формула (14.29);
– радиальный зазор с = с*m = 0,25m;
– угол профиля a = 20°.
Положительное эвольвентное зацепление представлено на рис. 14.18. Сопряженные эвольвенты изображены в трех точках. В начале зацепления в точке А2 соприкасаются ножка зуба шестерни и головка зуба колеса. В конце зацепления в точке А1 — головка зуба шестерни и ножка зуба колеса. В полюсе W показана одна из текущих фаз зацепления. Легко отметить перемещение точки контакта от ножки к вершине на шестерне и от вершины к ножке на колесе.
В любой фазе сопряженные эвольвенты имеют общую точку. По свойству эвольвенты производящая прямая всегда нормальна к эвольвенте. В случае сопряжения двух эвольвент в точке касания их производящие прямые совпадают. Следовательно, в этой точке они имеют одну общую нормаль. Она совпадает с общей касательной к обеим основным окружностям, т.е. с линией зацепления, которая не изменяет своего положения.
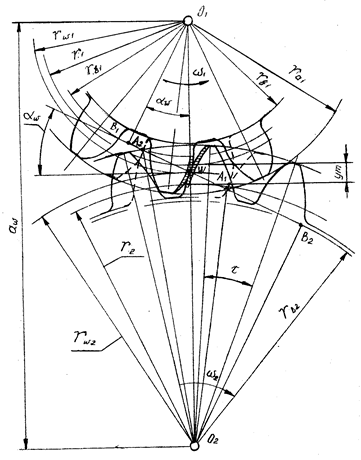
Рис. 14.18
Полюс зацепления, лежащий на линии зацепления, также не меняет своего положения. Следовательно, в эвольвентном зацеплении выполняется основная теорема зацепления: нормаль к сопряженным поверхностям зубьев проходит через одну и ту же точку на межосевой линии — полюс зацепления, что равнозначно постоянству передаточного отношения.
Также следует, что точка контакта сопряженных эвольвентных профилей может находиться только на линии зацепления. Она перемещается по линии зацепления от точки А2 к точке А1 (см. рис. 14.18).
NB 14.15. В эвольвентной зубчатой передаче полюс зацепления не меняет своего положения на межосевой линии, потому передаточное отношение постоянно на протяжении всего периода зацепления.
Для расчета геометрии эвольвентного зацепления используют уравнения эвольвенты в параметрической форме — формулы (14.9) и (14.10). На расчетной схеме (рис. 14.19) изображен профиль эвольвентного зуба. Начальная точка эвольвенты М находится на основной окружности. В точку М из точки О проведен радиус-вектор rb. По делительной окружности радиуса r толщина зуба определяется по формуле (14.28). На рис. 14.19 показана также произвольная окружность радиуса rу. По этой окружности толщину зуба обозначают sу.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.