, откуда
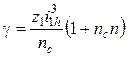= Ц, (15.7)
где Ц — любое целое число (1, 2, 3 и т.д.).
В простейшем случае при n = 0
=
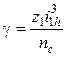Ц. (15.8)
Для редуктора Джеймса условие сборки (15.8) запишется так:
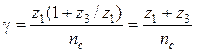= Ц. (15.9)
5. Условие правильного зацепления предполагает отсутствие интерференции зубьев зацепляющихся колес. Во внешнем зацеплении с нулевыми колесами при числах зубьев обоих колес больше 17 интерференция в виде заклинивания колес будет отсутствовать. Во внутреннем зацеплении интерференции не будет, если число зубьев колеса с внутренними зубьями z3 ³ 81, а шестерни с наружными зубьями z2 ³ 19, как следует из табл. 14.2.
NB 15.1. В планетарных механизмах выбор чисел зубьев ограничивается условиями соосности, соседства, сборки и правильности зацепления.
Задача определения чисел зубьев сводится к составлению исходных уравнений, отражающих условия синтеза для каждой конкретной схемы, и совместному их решению.
А. Редуктор Джеймса.
Для составления пропорции числа зубьев z2 и z3 и отношение g выражают через число зубьев z1. Число зубьев корончатого колеса z3 определяют по формуле (15.3). Число зубьев сателлитов z2 — из формулы (15.2) с учетом (15.3):
. (15.10)
Из условия сборки используют отношение g — формула (15.7). С учетом изложенного составляют пропорцию:
. (15.11)
Правую часть уравнения (15.11) умножают на nc/z1, получая пропорцию в окончательном виде:
. (15.12)
В соответствии с пропорцией (15.12) числа зубьев колес:
z1 = pnc;
z2 = p 
/2; z3 = p 
; g
= p
(1 – ncn).
(15.13)
В выражениях
(15.13) р — коэффициент, назначаемый в соответствии с ограничениями, и прежде всего z
17. После расчета чисел зубьев выполняют проверки по пяти условиям синтеза
(п. 15.2).
Пример 15.1.
Подобрать числа зубьев z1, z2,
z3 и КПД редуктора Джеймса (см. рис. 15.1) при = 6,5; nс = 3; h = 0,96.
Решение:
Составляем пропорцию (15.12):
.
Числа зубьев колес и отношение g находим из выражений:
z1 = 3p; z2 = 6,75p; z3 = 16,5; g = 6,5p (1 – 3n).
В соответствии с численными сомножителями необходимо принимать р, кратное 4; принимаем р = 8 из условия z1 > 17;
z1 = 3×8 = 24; z2 = 6,75×8 = 54; z3 = 16,5×8 = 132; g = 52 (1 – 3n).
Нетрудно видеть, что при р = 4 не выполняется условие неподрезания для центрального колеса (z1 = 3·4 = 12 < 17).
Проверки:
1) условие соосности — формула (15.1):
24 + 54 = 132 – 54; 78 = 78;
2) кинематическое условие — формула (13.3):
= 1 +
132/24 = 6,5;
3) условие соседства — формула (15.4):
(24 + 54) sin(180/3) – 54 = 13,55 > 2;
4) условие сборки выполняется, так как g — целое число при любых n (0, 1, 2 и т.д.); либо вторая проверка по формуле (15.9):
g
= 
= 78 — целое число;
5) во внутреннем зацеплении интерференция отсутствует, так как z2 > 19, z3 > 81 в соответствии с табл. 14.2. В зацеплении z2/z3 шестерней является колесо 2, а колесом — колесо 3.
Вывод:
Все условия выполнены.
Величину КПД определяем по формуле (13.7):
.
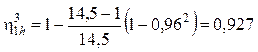Б. Эпигипоциклический механизм (см. рис. 13.5).
; z2/z1
= y, откуда
z2 = yz1; (15.14)
= xyz1. (15.15)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.