Учебное пособие по курсу "Теория механизмов и машин", страница 52

6. Определяют приведенный момент инерции I_п из условия равенства кинетических энергий 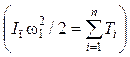 и строят диаграмму  в масштабе μ_I.

7. Диаграмма  в масштабе μ_I с началом координат в точке О одновременно является диаграммой кинетической энергии всех звеньев, кроме начального,  в масштабе .

8. От точки М наименьшей кинетической энергии Т_п проводят новую ось абсцисс. В новой системе координат с центром в точке М образуется диаграмма приращения кинетической энергии ΔТ_II = ΔT_II (φ).

9. Для определения момента инерции маховика I_М по методу Мерцалова строят диаграмму  путем вычитания из значений (или отрезков)  значений  с учетом масштабов.

10. Из точек наибольшего максимума и наименьшего минимума проводят линии, параллельные оси абсцисс, до пересечения с осью ординат в точках А и Б. Величина  дает наибольший перепад приращения кинетической энергии звена приведения, который должен взять на себя маховик, а момент инерции маховика равен . В целях ограничения габаритов маховика коэффициенту неравномерности  задают приемлемо малые значения.

8.9. Определение угловых скоростей звена приведения

Для определения закона движения начального звена применяют уравнение движения механизма в форме интеграла энергии — формула (7.8):

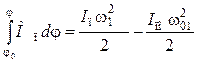, откуда

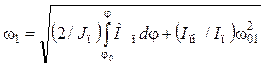                         .              (8.29)

Уравнение (8.29) решают численными методами на ПЭВМ или графическими методами, которые позволяют построить зависимость . Графическое решение является приближенным, но при коэффициенте неравномерности  ошибка оказывается настолько малой, что в инженерных расчетах ею можно пренебречь. Перепад кинетической энергии звена приведения с маховиком можно записать так:

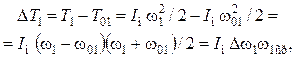                                    (8.30)

где  — угловая скорость звена приведения (кривошипа) в конце промежутка времени, ;  — то же, в начале промежутка; выражение  справедливо только при малых коэффициентах неравномерности.

Так как  и  — постоянные величины, то диаграмма  = (j) одновременно является диаграммой изменения угловой скорости  — график XI на рис. 8.3, г). Уравнение (8.30) можно записать в виде:

                                 ,                                откуда при равенстве ординат  масштаб угловой скорости в мм×с:

                                        .                             (8.31)

Линию средней угловой скорости проводят от середины отрезка АБ параллельно оси абсцисс. Начало координат тахограммы  не показывают, так как оно выходит за пределы чертежа. Фактическая угловая скорость для любого положения:

                                     ,                           (8.32)

где  — отрезок, измеряемый от средней линии диаграммы .

Определение закона изменения скорости звена по заданной нагрузке составляет задачу динамического анализа. Из рассмотренного следует, что изначальная посылка кинематического анализа о постоянной угловой скорости кривошипа не соответствует действительности. Колебания угловой скорости приводят к появлению углового ускорения и динамических нагрузок.

8.10. Определение угловых ускорений

Графическим или численным дифференцированием диаграммы  получают диаграмму углового ускорения кривошипа . Метод графического дифференцирования рассмотрен в теме 4.

По методу хорд на каждом участке диаграммы  кривые заменяют хордами. Параллельно им из полюса дифференцирования P₂, отложенного на отрезке дифференцирования Н₂ (40…60 мм), проводят лучи до пересечения с осью ординат. Полученные ординаты откладывают на серединах участков и соединяют плавной кривой. Масштаб диаграммы угловых ускорений в мм·с² по методу графического дифференцирования:

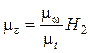                                           .                                 (8.33)

Масштаб времени определяют по формуле (4.34). По диаграмме  — график XII на рис. 8.3, е — величины угловых ускорений определяют делением длин отрезков в мм на масштаб. Известная величина  позволяет рассчитать динамический момент, обусловленный неравномерностью вращения:

                                     .                          (8.34)