Учебное пособие по курсу "Теория механизмов и машин", страница 28

Дифференцируя выражение (5.1) по времени, находят скорость:

                        .               (5.2)

После второго дифференцирования находят ускорение:

                                                        (5.3)

При равномерном вращении кривошипа (w₁ = const, e₁ = 0) уравнение (5.3) примет вид:

                                       .                               (5.4)

5.3. Шарнирный четырехзвенник

5.3.1. Метод замкнутых векторных контуров

Исходные данные: кинематическая схема (рис. 5.2), длины звеньев: l₁ — кривошипа, l₂ — шатуна, l₃ — коромысла, l₄ — стойки; положения (координаты) центров масс звеньев l_BS2, l_DS3; угловая скорость w₁ (e₁ = 0), положительное направление — против часовой стрелки; угловая координата j₁, отсчитываемая от оси x против часовой стрелки.

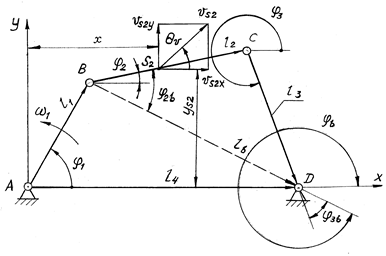
Рис. 5.2

Данный метод предложен В.А. Зиновьевым. При определении положения звеньев учитывают их ориентацию относительно осей координат с помощью векторов, связанных с соответствующими звеньями. Такой вектор связывают с осью звена, проходящей через оси его шарниров. Так, , , ,  (см. рис. 5.2). Такая методика носит название метод замкнутых векторных контуров.

NB 5.2. Метод замкнутых векторных контуров заключается в том, что каждое звено механизма связывают с вектором, проекции которого на координатные оси позволяют определить кинематические параметры.

Углы расположения векторов (направляющие углы) отсчитывают от оси x в направлении против часовой стрелки при условии нахождения начала вектора в центре шарнира. Для главного контура ABCD записывают очевидное векторное равенство:

                                                                        (5.5)

Проецируя уравнение (5.3) на координатные оси x и y, получают систему двух уравнений с двумя неизвестными j₂ и j₃:

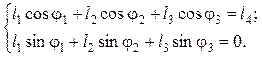                                            (5.6)

Систему уравнений (5.6) можно решить численными методами, так как искомые направляющие углы j₂ и j₃ присутствуют неявно. Существует и другой способ, когда j₂ и j₃ определяются в явном виде с использованием теорем синусов и косинусов и дополнительного векторного контура ВСD. Этот способ рассмотрен в следующем подпункте.

5.3.2. Определение направляющих углов

Дополнительно образуют базовый векторный контур, представляющий собой группу Ассура (диаду) 1-го вида, путем соединения крайних кинематических пар диады 2–3. Из точки B в точку D проводят базовый вектор l_b. Координаты точек B и D базового вектора:

                       x_B = l₁cosj₁; y_B = l₁sinj₁; x_D = l₄; y_D = 0.              (5.7)

Проекции базового вектора на координатные оси:

l_bx = x_D – x_B = l₄ – l₁cosj₁;                         (5.8)

                                   l_by = y_D – y_B = – l₁sinj₁.                           (5.9)

Длина базового вектора:

                        (5.10)

Вводят обозначения коэффициентов длины:

                               l₂ = l₂/l₁; l₃ = l₃/l₁; l₄ = l₄/l₁.                             

        (5.11)

                                              (5.12)

Направляющий угол базового вектора:

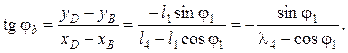                        (5.13)

Углы j_2b и j_3b, связывающие векторы и с базовым вектором , определяют по теореме косинусов из DBCD:

                                 ,                                откуда

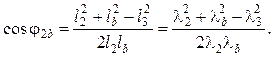                                        (5.14)

Аналогично получают:

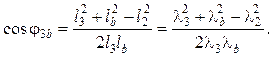                                        (5.15)

Направляющие углы j₂ и j₃ векторов и :

                                 j₂ = j_b +j_2b; j₃ = j_b – j_3b.                       (5.16)

После подстановки в формулы (5.16) выражений из (5.13)–(5.15) получают:

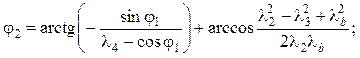                      (5.17)

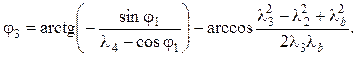                      (5.18)

Следует помнить, что направляющие углы отсчитывают от положительного направления оси x против часовой стрелки. При этом начало координат переносят в начало вектора.

5.3.3. Определение скоростей

Для определения угловых скоростей систему (5.6) дифференцируют по времени:

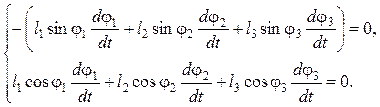                  (5.19)

Система уравнений (5.19) линейна относительно угловых скоростей  и . Учитывая, что  и коэффициенты λ₂ = = l₂/l₁ и λ₃ = l₃/l₁, получают систему в виде: