Машиностроение \ Теории механизмов и машин

Учебное пособие по курсу "Теория механизмов и машин", страница 106

Передаточное отношение — формула (13.13):

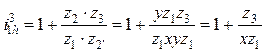                         ,                        откуда

                                       z3 = z1x ( – 1).                            (15.16)

Из условия соосности и формул (15.14) – (15.16) находят отношение y:

                                       z1 + z2 = z3 – ;                            (15.17)

                               z1 + yz1 = z1x ( – 1) – xyz1;                            

                                   1 + y = x ( – 1) – xy,                                  откуда

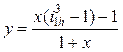                                       .                            (15.18)

Из условия размещения хотя бы двух сателлитов определяют границы коэффициента 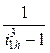х:

                                      < х < 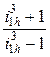.                         (15.19)

Общая расчетная пропорция

          .(15.20)

Пример 15.2. Подобрать числа зубьев z1, z2,  и z3 и КПД эпигипоциклического механизма (см. рис. 13.5) при  = 14,5; nc = 3; h = 0,96.

Решение:

Границы отношения х — формула (15.19):

                              

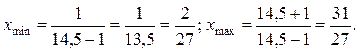
Принимаем х = . Коэффициент у — формула (15.18):

                                  .                                

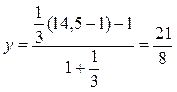В соответствии с пропорцией (15.20) записываем выражения:

              z1 = 3p; z2 = 3p = p; ;            

     z3 = ; g = 14,5p (1 – 3n) = .   

Принимаем р = 8. Числа зубьев и отношение g:

                           z1 = 3 × 8 = 24; z2 = 8 × 63/8 = 63;                         

                        = 8 × 21/8 = 21; z3 = 8 × 27/2 = 108.                     

                          g = 8 × 29 (1 – 3n)/2 = 116 (1 – 3n).                        

Проверки:

1)  z1 + z2 = z3 – z2; 24 +63 = 108 – 21; 87 = 87;

2)   = 1 + (z2z3)/(z1) = 1 +  = 14,5;

3)  (24 + 63) sin(p/3) – 63 = 12,3 > 2; (108 – 21) sin(p/3) – 21 = = 54,3 > 2;

4) g равно целому числу при любом n;

5) интерференции для  = 21 и z3 = 108 нет (см. табл. 14.2).

Вывод:

Все условия выполнены.

Анализ. Метод пропорций достаточно прост. Однако для получения оптимального по габаритам результата необходимо повторить расчеты с различными значениями х:  …  и выбрать вариант с наименьшим условным габаритом. Кроме того для удобства подбора коэффициента пропорциональности р необходимо вести расчеты с обыкновенными дробями. Также дробным может быть назначен и коэффициент р.

15.4. Подбор чисел зубьев с использованием ПЭВМ

Компьютерные расчеты позволяют рассчитать числа зубьев планетарного редуктора с любым передаточным отношением путем перебора чисел зубьев в задаваемых пределах от zmin до zmax. Основные принципы синтеза изложены в п. 15.1 и 15.2.

А. Редуктор Джеймса.

1. Записывают условие соосности (15.1) в виде:

z1 + z2 = z3 – z2 = d, откуда числа зубьев

                                            z1 = d – z2;                               (15.21)

                                            z3 = d + z2.                                (15.22)

В формулах (15.21) и (15.22) d — аналог межосевого расстояния;

                                а = 0,5m (z1 + z2) = 0,5md.                              

2. Из кинематического условия с учетом равенств (15.21) и (15.22) находят величину d:

                           = 1+ z3/z1 = 1 + (d + z2)/(d – z2),                        

откуда

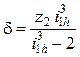                                            .                                (15.23)

3. Использование допускаемого отклонения передаточного отношения:

                          ,              (15.24)

где Di — отклонение передаточного отношения.

После подстановки выражений (15.24) в формулу (15.23) получают значения dmin и dmax.

4. Организация циклов.

В компьютерных расчетах внутренний цикл образуется изменением величины d, которая задается целыми числами в интервале dmin – dmax. По формулам (15.21) и (15.22) рассчитывают числа зубьев z1 и z3. При этом изменение чисел зубьев сателлитов z2 составляет внешний цикл.

Скачать файл