При последней попытке было выбрано некоторое усложнение нейронной сети. Была выбрана конфигурация, отображенная на рис. Рис. 54 (построено с помощью пакета Statistica Neural Network 4.0)
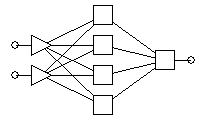
Рис. 54. Модифицированная конфигурация сети
После ряда запусков программы в окне Case Errors (Ошибки измерений) появилась следующая картина (рис. Рис. 55).
Поскольку в данном примере классификация производится по уровню 0,5 (если величина выхода меньше 0,5, то это значение принимается нулевым, а ситуация классифицируется как не требующая принятия мер; иначе - единичным), то допустимый уровень ошибки вычисления выхода составляет 0,5. Из рисунка видно, что ситуаций с ошибкой, большей 0,5 всего две: 50‑я и 70‑я. Их координаты соответственно 0,1; 0,9 и 0,9;0,9, то есть находятся на границах между областями.
Параметры готовой сети программа выдает в виде рис. Рис. 56.
Здесь IN1, IN2 – входы; OUT – выходной нейрон; h1#01, h1#02, h1#03, h1#04 – четыре нейрона скрытого слоя, то есть слоя, находящегося между входами и выходным слоем; Threshold – значение порога. Первая строка таблицы показывает значения порогов четырех скрытых и одного выходного нейрона, а остальные – веса связей между входами и нейронами или между нейронами.
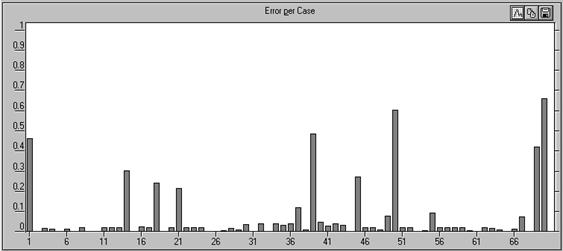
Рис. 55. Ошибки классификации для каждой ситуации
Данная нейронная сеть является наилучшей из полученных, так как она неправильно классифицирует обучающие ситуации только в двух случаях из семидесяти.
Для того, чтобы воспользоваться полученным классификатором, на его вход подается описание новой ситуации в координатах относительного потенциала рынка и относительной цены. Если полученный на выходе ответ меньше 0,5, то считается, что ситуация не нуждается в изменении, иначе – нуждается.

Рис. 56. Параметры результирующей сети
Подводя итоги исследованиям средств построения нейронных сетей на примере, можно сделать следующие выводы. Нейронные сети далеко не всегда приводят к хорошему решению; часто обучение попадает в тупик локального экстремума. Критериев для обнаружения такой ситуации, кроме визуального контроля, практически нет. Методы выхода из локального экстремума путем случайных воздействий не очень эффективны. В целом получение хорошей сети – дело везения.
Все это приводит к заключению, что нейронные сети следует использовать в случаях, когда другие методы оказались неэффективными, когда зависимость между входом и выходом сложна, а разделение на области не поддается простой графической интерпретации. Вот почему нейронные сети успешно применяются при распознавании образов: для распознавания важен каждый из многочисленных входов и сложная взаимосвязь между фрагментами изображения. Если эти признаки присутствуют в описании маркетинговой ситуации, имеется целый ряд аналогично описанных случаев с известными решениями, а схожие ситуации будут повторяться, то есть хорошие предпосылки использования нейронных сетей при принятии решений.
В данной главе все вышеизложенное обобщается в виде алгоритма выбора метода принятия решения. Алгоритм представлен в табличной форме (табл. 9). Вначале следует определить, к какому классу относится решение, которое следует принять. Для этого следует читать строки таблицы, отмеченные жирным шрифтом.
Затем, когда класс решений определен, в рамках данного класса выбирается конкретный метод. В таблицу включены и методы моделирования, так как они играют важную роль в принятии решений. Роль моделирования не исчерпывается описанием объекта управления.
Следует отметить, что данная таблица является лишь неким ориентиром, поскольку многообразие методов безгранично. Можно, например, построить имитационную модель с самонастройкой и, задав критерий оптимизации и набор изменяемых параметров, включить алгоритм, работающий по схеме: имитация—оценка—корректировка параметров, останавливающийся, когда оценка станет наилучшей. Здесь рассматриваются только методы «в чистом» виде, без необязательных дополнений.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.