В рамках метода сравнения с образцом в таблице исходных данных координаты каждой из имеющихся ситуаций были заменены координатами центра соответствующего кластера. Для этого использовалась таблица принадлежности ситуаций кластерам (таблица Cluster Membership).

Рис. 53. Количество ситуаций в каждом из
полученных кластеров
(последние две строки содержат соответственно
число полностью описанных ситуаций
и число ситуаций, для которых недостаточно данных)
Эти данные были использованы для настройки нейронной сети вида рис. Рис. 49 с помощью программы Panalyzer.
Было проделано 5 экспериментов по
обучению сети. Во всех случаях было найдено решение, классифицирующее центры
кластеров без ошибок. Число попыток, которое потребовалось для этого программе,
находилось в пределах от 1 до 5 [86].
Такая высокая степень успеха по сравнению с предыдущими попытками обучения
нейронной сети объясняется тем, что ситуации стали «разреженными»: если раньше
они образовывали «размытые» области (см. рис. 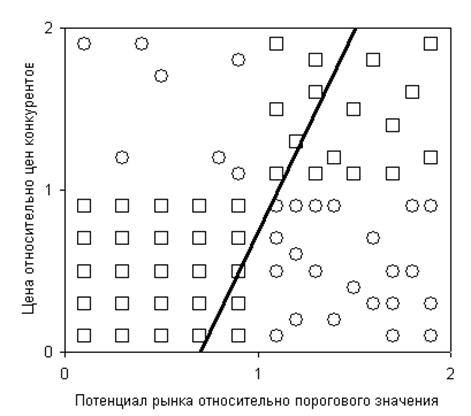
Рис. 44), то теперь каждая область заменяется одной точкой – центром соответствующего кластера. В такой ситуации легче найти подходящий набор значений параметров сети с помощью случайного поиска.
Для того, чтобы осуществить проверку полученного классификатора, он был использован для классификации имеющихся ситуаций без модификации их координат (относительной цены и относительного потенциала). При этом ошибка классификации составляла от 44 до 53%, что свидетельствует о том, что нейронная сеть работает неудовлетворительно.
5. Полученные результаты. Эксперименты показали, что и данная модификация метода не привела к построению хорошей нейронной сети. Но попутно был создан хороший классификатор по методу сравнения с прототипом, который классифицирует ситуацию по ее близости к одной из четырех типовых.
Третьей из рассмотренных программ построения нейронных сетей была система Statistica Neural Network 4.0, совместимая с известным пакетом Statistica. Это довольно мощная система, позволяющая строить нейронные сети различных типов большим количеством методов.
После ввода в программу уже известного набора исходных данных и структуры сети можно начать тренировку. В данной программе можно по желанию продолжить тренировку или начать заново с новыми, случайно задаваемыми значениями весов.
Использование обычного алгоритма обратного распространения привело практически к тем же результатам: вероятность ошибки прогноза даже для обучающих ситуаций осталась высокой.
Однако система Statistica Neural Network 4.0 реализует еще несколько алгоритмов обучения сети, среди которых – метод спуска по сопряженным градиентам (conjugate gradient descent). Вот его описание на основе материалов системы помощи пакета. Метод был предложен Бишопом в 1995 году и Шефердом в 1997 году и предназначен для обучения многослойных перцептронов. Указывается, что он работает лучше, чем метод обратного распространения, применяется в тех же ситуациях, что и последний, но особенно – для сложных случаев с более чем сотней весов. Если метод обратного распространения настраивает веса сети после каждого примера, метод спуска по сопряженным градиентам вырабатывает средний градиент поверхности ошибок по всем примерам, после чего производит обновление весов один раз за всю эпоху. Отмечается, что данный алгоритм проще в использовании, чем традиционный алгоритм обратного распространения, так как требует меньше настроечных параметров. Отмечается также, что скорость работы данного алгоритма примерно в 3 раза ниже, чем для алгоритма обратного распространения, однако для современных компьютеров это не является серьезным недостатком, а для данного простого примера вообще незаметно.
Но использование этого и еще пяти других методов также не дало ощутимого эффекта.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.