Принятие управленческих решений в маркетинге с помощью компьютерных средств, страница 24

круг – теоретические конструкции.

треугольник – наблюдаемые переменные.

прямоугольник – эмпирические концепции.

сплошная линия – гипотеза.

пунктир – правила соответствия.

волнистая линия – рабочее определение.

Пример гипотезы о поведении покупателя при покупке [52] дан на рис.6Рис. 6. Цель построения данной модели – определить, какие ментальные факторы влияют на поведение покупателя (потребителя). Если такая модель будет построена и окажется достоверной, можно будет

○  прогнозировать поведение покупателя по данным анкетирования;

○  определить, как и на какие ментальные факторы можно влиять, чтобы поведение изменилось в желательном для производителя и продавца направлении.

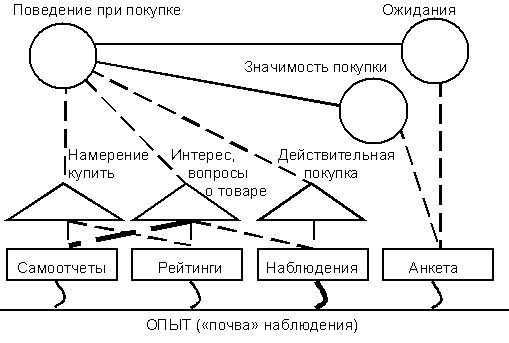
Рис. 6. Теория о поведении покупателя при покупке

В данном случае гипотеза заключается в том, что с поведением при покупке связаны ожидания от обладания товаром и значимость покупки. Все эти концепции не могут быть проверены непосредственно.

Значения связей пунктирных линий от треугольника к квадрату становится ясным из примера. Так, жирная пунктирная линия означает: Если у респондента Y попросить записать, сколько раз он спрашивал о товаре за последнюю неделю, то ответ будет z.

Значение жирной волнистой линии: Наблюдатель записывает, купил ли покупатель товар и в каком количестве.

Все связи в модели предполагаются линейными. Линейная модель проста, часто встречается в экономике, полезна в качестве первого шага анализа, часто достаточна, так как информация не очень достоверна. В общем случае каждая конструкция состоит из нескольких параметров. Например, ожидания складываются из степени удовлетворения определенной потребности, оценки удобства эксплуатации товара, его долговечности и т. д. Каждый из этих параметров влияет на каждый компонент действительной покупки (количество, периодичность, цена и т. д.). Ожидания имеют такие компоненты, как престижность владения товаром, снижение времени и повышение удобства выполнения определенной работы (например, при покупке нового стирального порошка улучшается процесс стирки). Таким образом, каждая связь описывается системой уравнений.

Наиболее удобно использовать для таких уравнений матричную форму.

Система [матричных] линейных уравнений, описывающих модель (гипотезу), называется структурными уравнениями.

Рис. 6. еще недостаточен для гипотезы. Требуется узнать силу связей и проверить, насколько эта гипотеза соответствует собранным данным. Иными словами, требуется определить параметры (коэффициенты) структурных уравнений. Все это делается по результатам опросов и наблюдений.

Существуют компьютерные средства для анализа таких моделей. Поддерживается как описание сети в виде набора утверждений, так и их визуализированное построение. После того, как структура модели, построенной исследователем, введена в компьютер с помощью специального языка, и введены результаты опросов и наблюдений всех наблюдаемых переменных, программа автоматически пытается найти такие значения коэффициентов модели (силу связей), которые обеспечат максимальное согласие данных измерения и гипотезы.

Для вычисления коэффициентов ставится задача сравнения реальных данных о выходных переменных и выходных данных модели.

Выполняются следующие шаги:

○  неизвестным параметрам присваиваются некоторые начальные значения;

○  по имеющимся входным данным (в примере – по результатам анкетирования) с помощью модели определяются выходные данные (ожидаемые значения наблюдаемых переменных);

○  проверяется соответствие полученных расчетным путем данных с данными, полученными при измерениях;

○  оценивается качество предсказания (совпадение реальных и расчетных выходных данных). Для оценки совпадения результатов можно использовать, например, критерий c²;

○  для нахождения более удачных значений параметров модели используются известные методы поиска экстремума.