Принятие управленческих решений в маркетинге с помощью компьютерных средств, страница 81

○  После очередного шага расчета последнее уравнение может дать величину, меньшую нуля. В этом случае эта величина заменяется нулем.

Приведенные корректировки несложно вести в алгоритм имитации. С учетом корректировок формулы для моделирования будут выглядеть следующим образом:

К1=З1*Б;
К2=З2*Б;
У1=ЕСЛИ(Н<0,001;0; ЕСЛИ ((Н*Р1+Н*И1*С+Н*Р2+
Н*И2*С)<Н;(Н*Р1+Н*И1*С);(Н*Р1+Н*И1*С)/(Н*Р1+
Н*И1*С+Н*Р2+Н*И2*С)*Н);
У2= ЕСЛИ (Н<0,001;0; ЕСЛИ ((Н*Р1+Н*И1*С+Н*Р2+
Н*И2*С)<Н;(Н*Р2+Н*И2*С);(Н*Р2+Н*И2*С)/(Н*Р1+
Н*И1*С+Н*Р2+Н*И2*С)*Н);
З1=З1-К1+У1;
З2=З2-К2+У2;
И1=И1+К1;
И2=И2+К2;
Н= ЕСЛИ ((Н-К1-К2+У1+У2)<0;0;(Н-К1-К2+У1+У2)).

Здесь введена нотация, аналогичная используемой в Excel: использована функция

ЕСЛИ(условие;выражение1;выражение2).

Результат применения этой функции равен выражению1, если условие истинно и выражению2 в противном случае.

Выбор интервала моделирования производится аналогично случаю уравнения в форме дифференциальных уравнений.

Шаг моделирования равен выбранной единице времени, то есть одному месяцу.

Решение задачи производится путем многократного расчета приведенных выше формул. Итоговые графики для исходных данных, совпадающих с решением системы дифференциальных уравнений, показаны на рис. Рис. 35.

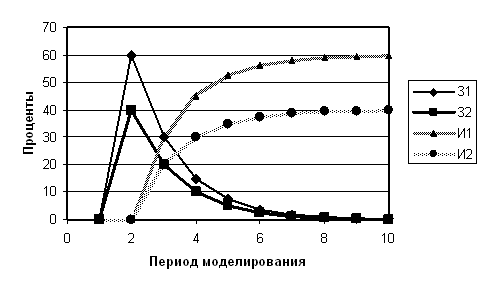
Рис. 35. Переходные процессы в системе с запаздыванием

Сравнение с графиками, полученными с помощью дифференциальных уравнений, очевидно, более точных, показывает, что качество переходных процессов сохранилось, их длительность и установившиеся значения – тоже. Таким образом, по данной модели можно сделать в основном те же выводы, что и по модели в виде системы дифференциальных уравнений.

Различия касаются:

○  максимальных значений количества знающих (по графику нетрудно подсчитать, что о товарах все узнали уже во втором периоде: о первом узнали 60%, о втором – 40%;

○  наличия запаздывания начала переходных процессов, которое появилось на рис. Рис. 35. Во-первых, расчет начинается не с момента времени t=0, а с шага (периода) 1, что является более привычным. Впрочем, можно считать исходное состояние шагом 0. Во-вторых, период 1 соответствует исходному состоянию, когда еще никто не знал о товаре, поэтому после первого шага его никто не купил.

Модель с запаздыванием позволяет построить график жизненных циклов товаров по их продажам на основании рассчитываемых значений К1 и К2. Он представлен на рис. Рис. 36.

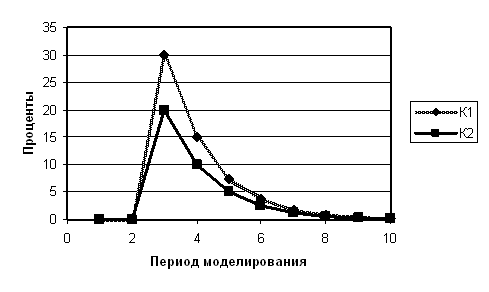
Рис. 36. Жизненные циклы товаров

На графике видна их длительность и высота.

Данная модель позволяет легко планировать величину затрат на рекламу по периодам. Для анализа различных вариантов следует лишь заменить константы Р1 и Р2 набором их значений по периодам. Это даже проще, чем производить расчеты по формулам для модели в форме дифференциальных уравнений.

Итак, использование моделей с запаздыванием проще для понимания менеджерами, так как они видят результаты и могут осуществлять планирование в привычной последовательности периодов, однако построение таких моделей несколько сложнее, чем моделей в форме дифференциальных уравнений, так как требует дополнительных рассуждений, допущений и не очевидных сразу корректировок формул.

В заключение следует отметить, что сохранение качества и большего числа количественных показателей при больших значениях шага моделирования свидетельствует о том, что решение дифференциальных уравнений на компьютере – не столь уж трудоемкая задача. Однако здесь возникают следующие проблемы:

○  проверка точности модели при большой величине шага. Для сложных моделей это совсем не тривиальная задача;

○  возрастание ошибки при усложнении модели, в частности – при объединении нескольких моделей в одну[78].