Принятие управленческих решений в маркетинге с помощью компьютерных средств, страница 77

Таким образом, предлагаемый учет знака управляющей связи позволяет сохранить преимущества когнитивной модели, сочетая их с наглядностью модели резервуаров.

7.1.4. Модель в форме дифференциальных уравнений

По рис. Рис. 32 и Рис. 33 довольно легко составить дифференциальные уравнения, описывающие задачу. Правда, при этом следует уточнить функциональные зависимости, отражаемые ранее только в виде наличия управляющих связей.

Для построения уравнений будет удобно ввести следующие условные обозначения:

Н – количество людей, не знающих о товаре;

З1 – количество людей, знающих о товаре фирмы 1;

З2 – количество людей, знающих о товаре фирмы 2;

И1 – количество людей, имеющих товар фирмы 1;

И2 – количество людей, имеющих товар фирмы 2;

Р1 – коэффициент воздействия рекламы фирмы 1: доля людей, не знающих о товаре, которые узнали о товаре фирмы 1 за единицу времени;

Р2 – коэффициент воздействия рекламы фирмы 2: доля людей, не знающих о товаре, которые узнали о товаре фирмы 2 за единицу времени;

С – коэффициент распространения слухов: количество обсуждений на одну пару, состоящую из человека, имеющего товар, и человека, не знающего о нем, за единицу времени;

Б – коэффициент благосостояния – доля людей, купивших товар, среди людей, знающих о нем, за единицу времени.

Производная обозначается символом «'».

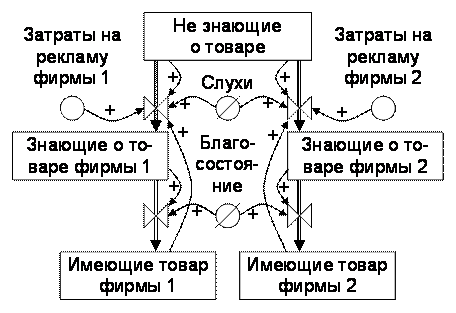
Рис. 33. Модель резервуаров, соединенных потоками,
в модифицированной нотации

Уравнения, описывающие систему, выглядят следующим образом:

Н'=-(Н*И1*С+Н*Р1)-(Н*И2*С+Н*Р2);
З1'=Н*И1*С+Н*Р1-З1*Б;
З2'=Н*И2*С+Н*Р2-З2*Б;
И1'=З1*Б;
И2'=З2*Б.

Они получены на основе рис. Рис. 33 и «здравого смысла» [75]. Первое уравнение показывает скорость убывания числа людей, не знающих о товаре. Поскольку это убывание происходит по двум потокам, имеются две составляющие, выделенные скобками. Знаки минус перед ними указывают, что количество людей, не знающих о товаре, уменьшается (потоки «вытекают» из «резервуара» не знающие). От чего зависит скорость уменьшения людей, не знающих о товаре, также видно из рис. Рис. 33. В скобках первое слагаемое показывает роль слухов: чем больше людей, не знающих о товаре, и людей, имеющих товар определенного вида, и чем больше интенсивность распространения слухов, тем выше скорость уменьшения количества людей, не знающих о товаре. Второе слагаемое отражает роль рекламы в этом процессе: чем выше затраты на рекламу и чем больше людей, не знающих о товаре, тем большее число узнает об определенном товаре из рекламы.

Содержимое вторых скобок в первом уравнении аналогично, но показывает роль фирмы 2.

Второе и третье уравнения описывают скорость изменения количества людей, знающих о товаре первой и второй фирмы, соответственно. С одной стороны, это количество растет за счет убывания количества людей, не знающих о товаре. Поэтому первые два слагаемых во втором и третьем уравнениях совпадают с содержимым скобок первого уравнения. Последнее слагаемое во втором и третьем уравнениях отражает уменьшение количества людей, знающих о товаре, но не имеющих его, за счет людей, купивших товар. Поэтому перед ним стоит знак минус. Скорость убывания количества людей, знающих о товаре (фактически это скорость покупок), равна количеству людей, знающих о товаре, умноженному на коэффициент благосостояния.

Четвертое и пятое уравнение показывают скорость увеличения количества людей, имеющих товар фирмы 1 и 2, соответственно. Из рисунка видно, что это увеличение происходит за счет уменьшения числа людей, знающих о товаре, но не имеющих его, поэтому левая часть уравнений совпадает с последними слагаемыми второго и третьего уравнений соответственно, но с обратным знаком.

Таким образом, по модели резервуаров, соединенных потоками, можно построить систему дифференциальных уравнений, описывающих систему.