Принятие управленческих решений в маркетинге с помощью компьютерных средств, страница 49

Пусть имеются две группы покупателей (А – покупающие товар типа 1, В – покупающие товар типа 2). Они характеризуются двумя признаками (X₁ – возраст, Х₂ – доход). В пространстве признаков группы располагаются, как показано на рис. 15Рис. 15. Задача состоит в том, чтобы найти правило разделения покупателей по группам в зависимости от значений характеризующих их признаков.

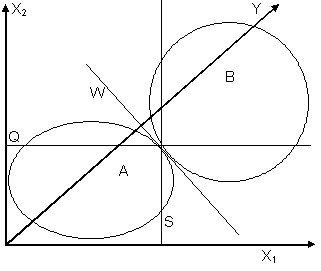
Рис. 15. Расположение групп покупателей различных товаров
в пространстве признаков

Разделение по признаку Х₁ с наименьшей ошибкой может осуществляться по линии S (если Х₁ больше порогового значения, то есть точка, соответствующая покупателю, находится правее S, то это В, иначе А), но из рисунка видно, что имеется некоторая ошибка такой классификации. Та же ситуация наблюдается и для классификации по признаку Х₂ (линия Q).

Но если построить новую ось Y (проекция каждой точки на ось Y будет равна n₁X₁+n₂X₂), то можно по значениям Y делить покупателей на группы А и В без ошибок. Разделительная линия обозначена как W.

Таким образом, дискриминантный анализ дает линейную комбинацию исходных признаков и пороговое значение, которое позволяет наилучшим образом разделять объекты на группы по значениям их признаков. Все расчеты производятся с помощью компьютера по известному набору случаев, а далее результат может быть использован для классификации новых объектов (покупателей, ситуаций, требующих решения и т.д.).

Если области пересекаются, как на рис. 16Рис. 16, то можно построить линию W, дающую наименьшую, но ненулевую ошибку классификации.

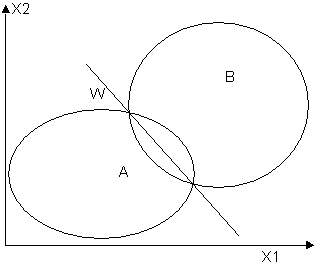
Рис. 16. Случай пересекающихся областей

Проблема применения метода состоит в том, что линия W строится по имеющимся образцам, а используется для классификации новых объектов. Ошибка классификации минимизируется для обучающих образцов и может быть довольно значительной для новых. Эта ситуация показана на рис. 17Рис. 17.

Для оценки важности той или иной переменной для классификации существует несколько способов.

○  Сильное влияние некоторой переменной можно выявить по заметному различию в средних значениях этой переменной среди различных групп.

○  Можно рассмотреть корреляцию значений между значениями каждого параметра X_k и Y. Большие ее значения отражают сильное влияние данной переменной.

○  Коэффициенты линейной комбинации также отражают вклад переменной в разбиение на группы. Чем больше некоторый коэффициент (вес переменной), тем более важна соответствующая ему переменная. Для сравнения относительной важности переменных следует использовать стандартизированный вес n_k*, определяемый по формуле:

n_k*=s_kn_k,

где s_k – среднеквадратическое отклонение k-й переменной, оцененное по выборке. Если стандартизированный вес мал, то либо переменная действительно оказывает малое влияние, либо имеется мультиколлинеарность (корреляция между признаками).

Рис. 17. Построение классификатора по имеющимся образцам

Если X_k мультиколлинеарны, то выводы по трем критериям будут различными, и следует выбрать другие признаки классификации, если независимы, то все подходы дадут сходный результат, который и можно принять за окончательный.

Если число групп больше двух, то анализ несколько усложняется. Классический подход заключается в построении дискриминантных функций, дающих максимальные различия между каждой парой групп. Канонический подход связан с построением одного дискриминанта на все группы. Таких дискриминантных функций может быть построено несколько. Критерий определения Y для этого случая равен:

J = дисперсия Y между классами/дисперсия Y внутри классов à max.