Принятие управленческих решений в маркетинге с помощью компьютерных средств, страница 78

Для решения построенной системы следует указать начальные условия. Согласно сделанным допущениям, вначале о товарах предлагаемого фирмами типа никто не знает, поэтому число людей, не знающих о товаре, равно численности населения, а начальные значения переменных З1, З2, И1, И2 равны нулю. Удобно также решать уравнения, перейдя от численности населения к процентам. Это можно сделать, так как численность населения предполагается постоянной. Итак,

Н(0)= 100(%);
З1=0;
З2=0;
И1=0;
И2=0.

Если решение производится не с помощью специализированных средств, а, например, средствами Excel, то следует вручную перейти к разностной форме, используя определение производной:

.

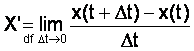В данном случае следует перейти от производных к конечным разностям:

(H(t+Δt)-Н(t))/Δt=-(Н(t)*И1(t)*С+Н(t)*Р1)-(Н(t)*И2(t)*С+Н(t)*Р2);
(З1(t+Δt)-З1(t))/Δt=Н(t)*И1(t)*С+Н(t)*Р1-З1(t)*Б;
(З2(t+Δt)-З2(t))/Δt=Н(t)*И2(t)*С+Н(t)*Р2-З2(t)*Б;
(И1(t+Δt)-И1(t))/Δt=З1(t)*Б;
(И2(t+Δt)-И2(t))/Δt=З2(t)*Б.

Отсюда путем умножения на Δt и переноса значения переменных в момент t в правую часть каждого уравнения могут быть получены итеративные формулы пересчета значений всех переменных:

H(t+Δt)=Н(t)-(Н(t)*И1(t)*С+Н(t)*Р1+Н(t)*И2(t)*С+Н(t)*Р2)*Δt;
З1(t+Δt)=З1(t)+(Н(t)*И1(t)*С+Н(t)*Р1-З1(t)*Б)*Δt;
З2(t+Δt)=З2(t)+(Н(t)*И2(t)*С+Н(t)*Р2-З2(t)*Б)Δt;
И1(t+Δt)=И1(t)+З1(t)*Б*Δt;
И2(t+Δt)=И2(t)+З2(t)*Б*Δt.

Построить решение такого уравнения с учетом начальных условий не составляет труда. На рис. Рис. 34 показан вид переходных процессов[76] для переменных З1, З2, И1, И2 при указанных выше начальных условиях и Δt=0,01 единицы времени. В качестве единицы времени выбирается 1 месяц. Значения коэффициентов равны: С=0,5; Р1=0,6; Р2=0,4; Б=0,5.

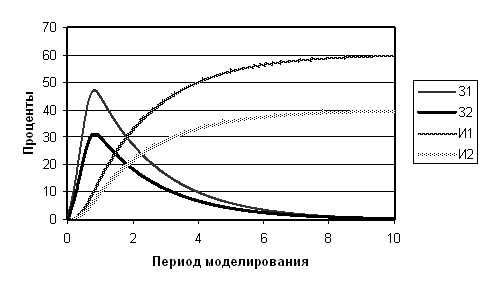
Рис. 34. Переходные процессы в моделируемой системе.

Из рисунка видно, что количество людей, имеющих товар каждой из фирм, вначале растет медленно, затем этот рост ускоряется, а в конце процесса вновь замедляется. К 1000 шагу моделирования (к концу десятого месяца) число людей, имеющих товар, практически не изменяется, что говорит о том, что продажи почти прекратились. Число людей, знающих о товаре, но не имеющих его, имеет максимум примерно в конце месяца 1, а затем спадает, так как рост этого числа замедляется (уже очень многие знают о товаре), а переход людей в категорию купивших товар уменьшает количество знающих о товаре, но не имеющих его.

Для оценки объема продаж по графикам можно использовать тот факт, что объемы продаж каждого и товаров пропорциональны количеству знающих о товаре, что следует из исходных дифференциальных уравнений, описывающих моделируемую систему.

Интервал моделирования подбирается в данном случае эмпирически. Если переходные процессы (изменения переменных от времени) еще не закончились, моделирование продолжается.

Шаг моделирования Δt необходимо откорректировать в случае, если его длительность сравнима с длительностью переходных процессов. Минимальное значение шага должно быть в 20 раз меньше самого быстрого переходного процесса. В данном случае длительность переходных процессов составляет 10 месяцев, поэтому минимально возможное значение Δt составляет 0,5 месяца. Использованное значение Δt=0,01 с запасом обеспечивает точность моделирования. Однако величина Δt имеет еще одно ограничение. При больших значениях Δt может возникнуть выход переменных за их смысловые ограничения. Например, при большой длительности шага моделирования число узнавших о товаре двух видов может превысить число не знающих о товаре, что приведет на следующем шаге к отрицательному значению количества не знающих о товаре. В результате вид переходных процессов не будет иметь ничего общего с реальностью. Обычно при этом возникают расходящиеся колебания. Так что начинать следует с малых значений Δt. Если оказывается, что ресурсов компьютера не хватает, например, для рассматриваемой задачи за 1000 шагов переходные процессы только начались, то нужно уменьшать величину Δt до тех пор, пока не возникнет вышеописанная ошибка. Для рассматриваемой задачи уже при Δt=0,05 возникают расходящиеся колебания, и значение количества не знающих о товаре достигает значения (-8·10³⁵) вскоре после двухсотого шага.