Принятие управленческих решений в маркетинге с помощью компьютерных средств, страница 70

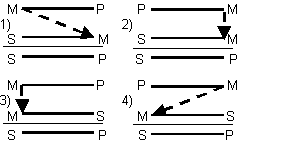
Рис. 29. Фигуры силлогизмов

Пример истинного силлогизма – ААА для фигуры 1 имеет вид

Всякий М есть Р        Всякий бытовой пылесос есть бытовой прибор.
Всякий S есть M        Всякий бытовой прибор есть предмет
                                   потребления.
Вывод
Всякий S есть P        Всякий бытовой пылесос есть предмет
                                   потребления.

В дальнейшем он будет обозначаться как 1 ААА.

Исходя из тех же посылок, можно также сказать, что некоторый S есть P (бытовые пылесосы есть предметы потребления). Если имеется два высказывания относительно одних и тех же сущностей и разница между высказываниями состоит только в том, что одно включает квантор всякий, а другое – некоторый, то первое высказывание называется сильным, а другое – слабым. Сильное высказывание «поглощает» слабое.

Истинными являются высказывания

Жирным цветом выделены сильные высказывания.

Сориты (силлогизмы с числом посылок более двух) моделируют процесс сложных рассуждений. Сущность их решения состоит в том, что выбираются пары высказываний, образующих посылки одного из корректных силлогизмов. Затем среди посылок появляется результат этого силлогизма и процесс повторяется. Завершается он тогда, когда больше нет условий для выполнения силлогизма.

Процесс анализа ситуации может начинаться с набора имеющихся данных в виде утверждений и иметь целью получение всех возможных корректных утверждений. Другой вариант – начать с тех утверждений, которые надо доказать. Тогда цель состоит в определении того, истинно ли доказываемое утверждение или того, какие утверждения необходимо проверить, чтобы убедиться в истинности целевого утверждения.

Из приведенного краткого описания видно, что процесс дедуктивных рассуждений достаточно трудоемок и сложен, хотя и подчиняется жестким правилам. Поэтому предпринимаются попытки автоматизировать его. Действительно, можно автоматизировать решение соритов или поиск доказательств некоторого высказывания. При этом можно быть уверенным в том, что все преобразования высказываний будут выполнены корректно.