Принятие управленческих решений в маркетинге с помощью компьютерных средств, страница 10

В процессе принятия решений используются и другие математические методы. Из них важна группа методов прогнозирования.

1.4.  Прогнозирование. Эта группа методов предназначена скорее не для разработки решения, а для получения информации. Прогнозирование разделяется на два вида.

1.4.1.  Предсказание будущего состояния процесса. Для этого используются следующие методы.

○  Линейная экстраполяция. Ищется функция вида x(t)=at+b, наилучшим образом соответствующая изменению переменной x во времени. Метод используется чаще других ввиду его простоты и того факта, что он достаточно хорошо показывает главные особенности будущего поведения исследуемого объекта (коэффициент a показывает, увеличивается или уменьшается прогнозируемая характеристика и насколько быстро; параметр b характеризует начальное значение x).

○  Нелинейная экстраполяция. Наиболее часто используются следующие функции, соответствующие наблюдаемым в экономике и маркетинге процессам:

·  экспоненциальная экстраполяция функцией вида x(t)=е^bt. Общеизвестно, что этой функцией в течение многих лет аппроксимировалось изменение важной характеристики такого популярного товара, как компьютеры: их быстродействие удваивалось каждые 18 месяцев[7];

·  кривая Перла была разработана в результате наблюдения за организмами и популяциями. Ее уравнение x(t)=L/(1+ae^-bt). При L=1, a=1, b=1 кривая имеет вид, показанный на рис. 3Рис. 3, а.

·  кривая Гомперца хорошо моделирует рост дохода, смертность. Ее уравнение:

,

а вид при L=1, b=1, k=1 показан на рис.3Рис. 3, б.

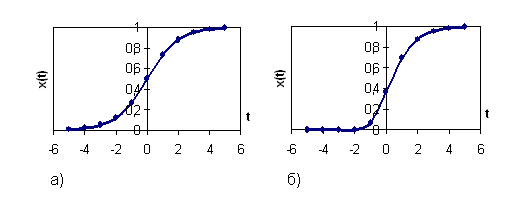
Рис. 3. Вид некоторых типовых экстраполяционных кривых

○  Моделирование. Оно дает более точные результаты, чем экстраполяция, так как основывается на идеях о структуре объекта, зависимостях между переменными, которые можно проверить по прошлому поведению. Поэтому при возможности выбора моделированию отдается предпочтение перед экстраполяцией[8]. Для принятия маркетинговых решений характерно использование следующих видов моделей.

·  Динамические модели. Объект описывается системой дифференциальных уравнений. Это позволяет, во-первых, определить качество протекающих в нем процессов (например, наличие колебательности), а во-вторых – получить ход развития процессов во времени.

·  Имитационное моделирование методом Монте-Карло, когда реализуется алгоритм случайного поведения объектов. Метод обычно применяется для систем массового обслуживания.

1.4.2.  Предсказание значений одних переменных по значениям других. Для этого применяются:

○  дискриминантный анализ;

○  факторный анализ[9].

○  оценка индекса предсказательной связи и других показателей качества предсказания.

1.5.  Статистика социально-экономических явлений. Изучает количественную сторону массовых социально-экономических явлений и процессов, определяя количественные зависимости, тенденции и закономерности. Ее результаты используются для прогнозирования и построения моделей.

1.6.  Анализ предельных показателей.

1.7.  Анализ эластичности функции.

2.   «Не совсем математические» методы. Для них нет доказательства их правильности и/или строгих оценок эффективности. Их применимость и полезность оценена только на основе опыта.

2.1.  Эвристики. Это алгоритмы, правильность которых не доказана. Пример – симплекс-поиск экстремума [14]. Они работают неплохо, основываясь на «логичных» идеях.

2.2.  Искусственный интеллект. По определению [33], искусственный интеллект – это алгоритмическая реализация некоторых операций по обработке информации, отличающаяся концепцией анализа задачи и построения (используется терминология описания знаний и работы с ними). Результатом применения алгоритмов искусственного интеллекта может явиться способность системы управления к улучшению своего функционирования или решению задач, не алгоритмизируемых обычными методами.