Теперь можно интерпретировать модель, изображенную на рис.7Рис. 7, а. Изменение численности населения (X) зависит от уровня рождаемости b и уровня смертности a, которые считаются постоянными. Если уровень рождаемости превышает уровень смертности, то уровень в резервуаре (численность населения) будет повышаться, и наоборот[30].
Проще всего считать, что время дискретно, имеет шаг Δt, а константы через управляющие связи задают объем, проходящий по каналу за один такт. В этом случае модель отображает разностное уравнение первого порядка:
X0=X(0); Xt+Δt = Xt+ΔХ = Xt+(b-a).
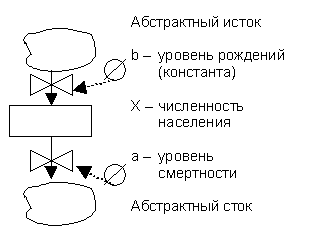
а)
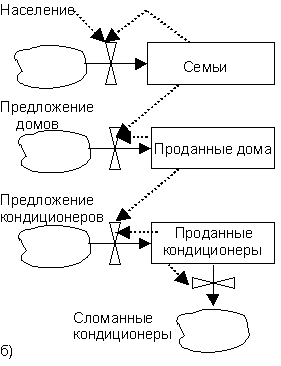
Рис. 7. Модели резервуаров, соединенных потоками
На рис. Рис. 7, б показана более сложная модель, также взятая из [59] и отражающая динамику продаж кондиционеров. Скорость изменения количества семей зависит от численности населения (если населения много, количество семей увеличивается быстрее) и имеющегося количества семей (чем больше семей уже создано, тем медленнее увеличивается их количество). Аналогичная картина наблюдается с проданными домами, которые покупают семьи (предложение домов считается в этой модели потенциально неограниченным), и к продаваемыми в дома кондиционерами. Наконец, чем больше имеется кондиционеров, тем большее их количество выходит из строя за единицу времени.
В последнем примере имеются как положительные, так и отрицательные управляющие связи. Возможно введение управляющих связей в форме более сложных функциональных зависимостей. Таким образом, метод применим для широкого класса сложных задач.
Из этой модели также несложно получить разностное уравнение, а из него, в свою очередь – дифференциальное[31]. «Решая дифференциальные уравнения, можно забыть о содержательном смысле переменных и использовать математический аппарат, разрабатываемый в течение столетий целым рядом выдающихся математиков. Используя их результаты, можно исследовать особенности поведения решений, получить качественные оценки» [36].
Практика показала, что для исследования социальных процессов ввиду их сложности недостаточно когнитивных моделей и аналитических методов. Если полученные уравнения слишком сложны или их аналитическое решение невозможно, большую помощь оказывает имитация поведения описываемых этими уравнениями систем и процессов. Компьютерные имитационные модели оказались более адекватными инструментами их исследования. В них становится возможным ввести ограничения, нелинейности и сложные алгоритмы поведения. Уже довольно давно созданы имитационные динамические модели национальных экономик и мирового развития [59].
Имитационное моделирование с помощью динамических моделей (т.н. системная динамика) является мощным инструментарием исследования динамических процессов, ориентированным на применение компьютеров [36].
Наконец, важным аспектом принятия управленческих решений является визуализация динамики управляемых процессов при различных управляющих воздействиях на объект управления. Этот процесс называется иногда иконологическим моделированием [36]. Из полученных графиков можно получить наглядную информацию для исследования сложных нелинейных систем.
Для того, чтобы использовать динамическое моделирование в принятии решения, следует руководствоваться общей схемой применения моделирования.
1. Определить, для решения какой проблемы строится модель. Критерием применения динамического моделирования является непрерывность переменных и непрерывность времени. Обычно динамическое моделирование применяется для анализа
○ поведения экологических систем в мировом или региональном масштабе;
○ динамики демографической ситуации;
○ социальных процессов;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.