А И В = НЕ (НЕ А ИЛИ НЕ В).
Между тем, эксперты-маркетологи редко категоричны с своих суждениях. Чаще они оперируют словами: может быть, наверное, наверняка, вряд ли, сомнительно, очевидно, почти никогда, практически всегда, то есть в этой области многое так и остается нечетким.
Чтобы оперировать с этими мнениями было введено понятие возможность[46], которая находится в диапазоне от 0 до 1. Если логические величины могут принимать любое значение из этого диапазона, то такая логика называется нечеткой.
Следующим шагом в создании нечеткой логики стало определение операций над нечеткими логическими переменными. Чтобы понять эту проблему, можно обратиться к распространенному представлению логических операций как комбинации ключей или вентилей. На рис.12Рис. 12, а представлена логическая операция И, а на рис.12Рис. 12, б – ИЛИ.
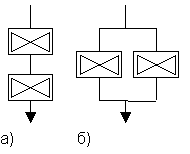
Рис. 12. Представление логических операций как комбинации ключей
Линии со стрелками представляют некоторый поток, а прямоугольники – вентили, которые могут быть либо открыты (ИСТИНА), либо закрыты (ЛОЖЬ). Видно, что для того, чтобы поток достиг выхода (чтобы результат был истинным), на рис.12Рис. 12, а должны быть открыты оба вентиля, а на рис.12Рис. 12, б – хотя бы один.
Если ввести еще одно логическое значение, МОЖЕТ БЫТЬ, возможность которого равна 0,5, то можно рассмотреть, как будет работать вентильная схема при полуоткрытых вентилях. Если на Рис. 12, а один вентиль открыт полностью, а второй – наполовину, то естественно предположить, что и результат (выходной поток) будет половинным. Если же аналогичная ситуация имеет место для схемы Рис. 12, б, то поток, очевидно, будет полным. Более сложны случаи, когда оба вентиля полуоткрыты.
Для работы с нечеткой логикой был предложен ряд формул, описывающих логические операции над нечеткими величинами. Наиболее распространенные выглядят как
а И b = min (a, b),
a ИЛИ b
= max (a, b).
Нетрудно убедиться, что при значениях переменных, равных 0 или 1, они работают как обычные операции И и ИЛИ. Используются и более сложные формулы [64].
Такой аппарат позволяет рассчитать возможность наступления сложного события, являющегося комбинаций нескольких простых, для которых существует оценка возможности.
В практике управления маркетингом часто встречаются многокритериальные задачи, в которых требуется достичь целого ряда целей. Чаще всего такая ситуация возникает при выборе из некоторого набора готовых альтернатив, например, при выборе информационной системы для маркетинга. В этом случае требуется, чтобы система была как можно дешевле, как можно удобнее в работе, как можно надежнее и т.д. Естественно, что одни цели (и соответственно критерии) более важны, другие – менее.
При возникновении такой задачи следует:
1. Определить важные для выбора параметры. При выборе информационной системы к их числу относятся: стоимость, функциональные возможности, опыт работников предприятия, гибкость, масштабируемость, эксплуатационные расходы и многое другое[47].
2. Устранить зависимость критериев. Это, как отмечается в [24], является большой проблемой. Критерии называются зависимыми, когда важность одного критерия зависит от значения другого. Например [24], при выборе дачи близость продовольственного магазина важна, если дача далеко от города (это – другой важный критерий выбора) и не очень важна, если дача близко от города. В этом случае следует попытаться объединить зависимые критерии в один. Для приведенного примера важна в конечном счете обеспеченность продуктами. Она высока, если дача близка от города или поблизости от нее имеется магазин. Таким образом, критерий близости магазина заменяется на критерий обеспеченностью продуктами. Критерий расстояния до города остается, так как представляет самостоятельную ценность при выборе.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.