Была выдвинута гипотеза о том, что область, из которой возможно обучение «правильным» значениям параметров сети, слишком узка. Чтобы устранить эту причину неудач, был использован известный метод сравнения с прототипом [17].
Суть метода сводится к тому, что каждый элемент исследования заменяется «типовым представителем» своего класса. Здесь предлагается один из многочисленных вариантов применения данного метода.
Выделение классов ситуаций проводилось с помощью кластерного анализа.
Таблица исходных данных со сведениями о семидесяти имеющихся ситуациях была введена в пакет SPSS 11.5, в котором был осуществлен иерархический кластерный анализ (Hierarchical Cluster).
1. Определение числа кластеров. В качестве переменных для кластеризации были выбраны все три переменные: относительная цена, относительный потенциал и решение (0 – не изменять, 1 – изменять). Это делается для того, чтобы различать соседние точки, если они требуют разного решения. Все значения были предварительно нормированы в диапазон от 0 до 1 (путем задания вида начального преобразования переменных)[84]. В качестве меры расстояния было выбрано евклидово расстояние, в качестве правила кластеризации – полная кластеризация (в пакете SPSS она называется Nearest Neighbor – по самому дальнему соседу).
На первом шаге кластерного анализа была получена таблица хода кластеризации (Agglomeration Schedule), из которой интерес представляет столбец Coefficients (коэффициенты). Эти коэффициенты показывают, насколько близки объединяемые кластеры. Число коэффициентов равно 69, так как для 70 ситуаций именно столько объединений нужно, чтобы все ситуации образовали один кластер. Значения коэффициентов представлены на рис. Рис. 51.
Из рисунка видно, что коэффициент резко увеличивается после шага 66. Поэтому в данных выделяется 70 – 66 = 4 кластера. Таким образом, первая часть задачи решена: кластерный анализ сумел выделить из представленных данных четыре типовых ситуации [85].
2. Формирование кластеров. Следующим шагом стало определение принадлежности каждой ситуации какому-либо кластеру и нахождение центров каждого кластера. Для этого была использована процедура разбиения на заданное число кластеров (k-Means Cluster). Число кластеров было задано равным четырем, согласно результатам шага 1.
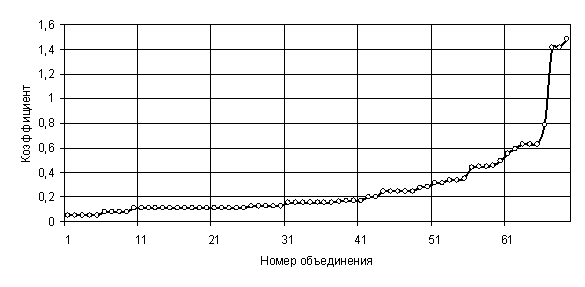
Рис. 51. Графическое отображение значений
коэффициентов
из таблицы хода кластеризации
Координаты центров полученных кластеров видны в таблице на рис. Рис. 52., а количество ситуаций в каждом кластере – на рис. Рис. 53. Для каждой ситуации можно вывести и номер кластера, которому она принадлежит (таблица Cluster Membership). Здесь эти данные не приводятся ввиду их громоздкости. Но из этой таблицы можно увидеть, что кластеры соответствуют клеткам таблицы решений (см. табл. Таблица 7)
3. Построение классификатора на основе расстояний до центров кластеров. Для новой ситуации можно определить, к центру какого кластера она ближе. Для этой оценки используются только причинные переменные. Координаты центров кластеров приведены в первых двух строках таблицы на рис. Рис. 52. Для расчетов предлагается использовать евклидово расстояние. По решению для ближайшего соседа принимается решение о классификации. Решение для каждого кластера дано в третьей строке таблицы на рис. Рис. 52.
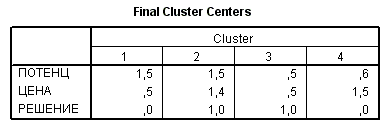
Рис. 52. Координаты центров полученных кластеров
Расчеты показали, что все имеющиеся ситуации классифицируются правильно. Однако для новых ситуаций возможны ошибки.
4. Построение классификатора на нейронной сети. Еще один из способов построения классификаторов – применение нейронных сетей. В общем случае в пользу его применения говорит сложная структура кластеров (большое их количество и «запутанное» расположение), что можно выявить при визуализации имеющихся данных.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.