Пусть имеем дифференциал, вал водила которого связан с двигателем, а два других – с ведущими колёсами. Из условия сохранения энергии получим:
![]()
или
![]()
где
![]() соответственно, мощность вала
водила, мощность
соответственно, мощность вала
водила, мощность
вала левого колеса, мощность вала правого колеса,
мощность потерь на трение в дифференциальном
механизме;
![]() соответственно, крутящие моменты на
валу водила,
соответственно, крутящие моменты на
валу водила,
на валу левого колеса, на валу правого колеса;
![]() соответственно, угловые скорости
валов водила,
соответственно, угловые скорости
валов водила,
левого и правого колёс.
Из условия равновесия внешних сил имеем:
![]()
Из уравнения скоростей дифференциального механизма при главном передаточном отношении, равном минус единица, получим:
![]()
Из написанных уравнений определим:
![]()
Подставим полученные значения момента на валу водила и угловую скорость этого вала в уравнение, полученное из условия сохранения энергии.
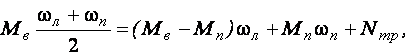
или
![]()
или
![]()
Решим последнее уравнение относительно крутящего момента на валу правого колеса.
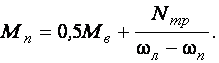
Используя это уравнение и уравнение, полученное из условия равновесия внешних сил, определим:
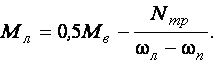
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.