Комплексное усиление пропускной и провозной способности железных дорог. Основные принципы организации и управления пассажирскими перевозками. Пригородные пассажирские перевозки, страница 67

Введем матрицу увязок :

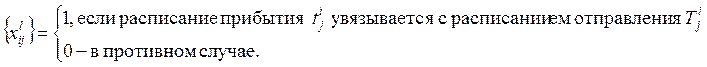
Матрица 39.1

Так как каждое расписание прибытия  может быть увязано не более чем с одним расписанием отправления и, наоборот, каждое может быть увязано не более чем с одним , имеют место неравенства:

, т. е. в каждом ряду матрицы увязок содержится не более одной единицы.

На основе матрицы возможных увязок учитывая приведенные неравенства, строим матрицу увязок

Для рассматриваемого примера представлена матрица увязок 39.2.

Матрица 39.2

Для рассматриваемого примера является началом, а  – концом маршрута. Очевидно, что в общем случае начало и конец одного маршрута могут находиться на разных станциях оборота. Маршрутом называется последовательность ниток графика движения увязанных между собой, по начальным и конечным станциям.

Построение маршрутов следования поездов осуществляется следующим образом. Находим начало маршрута (расписание отправления поезда) на некоторой станции оборота. Затем, используя информацию о поездах, находим номер поезда, номер станции назначения и расписание прибытия поезда на эту станцию. С помощью матрицы увязок \ ниток графика для данной специфики оборота увязываем полученное расписание прибытия поезда с расписанием отправления следующего поезда, входящего в маршрут, и так далее до тех пор, пока не выйдем на конец маршрута. При этом в каждом маршруте должно быть обеспечено необходимое время для проведения технического осмотра ТО-2. Маршрут, в котором состав заходит в депо для проведения профилактического осмотра и ремонта, назовем ремонтным.

Построив таким образом, все маршруты, увязываем их в единый замкнутый цикл (гамильтонов контур в графе маршрутов), обеспечивая тем самым равномерность использования подвижного состава и ритмичность работы депо. При построении гамильтонова контура маршрутов следует также обеспечить равномерное чередование ремонтных маршрутов. Этим достигается построение единого графика оборота пригородных составов с равным межремонтным пробегом составов.

Для пригородного участка с четырьмя станциями оборота пригородных составов при заданных нитках графика движения (рис. 39.7) построить единый график оборота пригородных составов, считая, что ,.

Рисунок 39.7 – Исходные данные для примера построения графика оборота

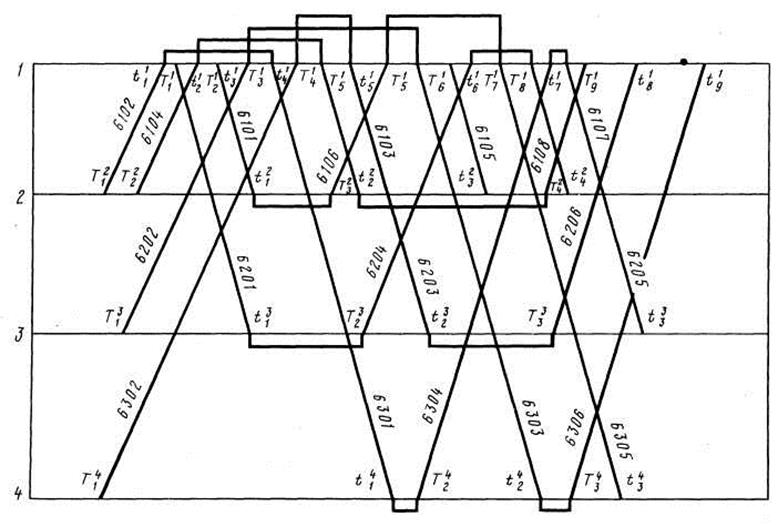
Определяем индексы к отрезкам временной оси (рис. 39.8).

Строим матрицы возможных увязок для первой (матрица 39.3), второй (матрица 39.4), третьей (матрица 39.5), четвертой (матрица 39.6) станций оборота.

Находим матрицу увязок 39.7 для первой, второй (матрица 39.8), третьей (матрица 39.9), четвертой (матрица 39.10) станций оборота. Увязка ниток показана на рис. 39.9.

Определяем: ;  ;; ; ; ;  – начала маршрутов; ; ; ; ; ; ; – концы маршрутов.

Строим маршруты следования поездов (табл. 39.11)

Находим гамильтонов контур маршрутов (см. рис. 39.10). Граф маршрутов – связный, поэтому можно построить гамильтонов контур. Очередность маршрутов в гамильтоновом контуре, например, следующая: 1, 5, 3, 4, 6, 2, 7. Перенумеруем маршруты в соответствии с их очередностью в гамильтоновом контуре. Тогда единый график оборота пригородных поездов будет иметь вид табл. 39.12.