Матрица 38.3
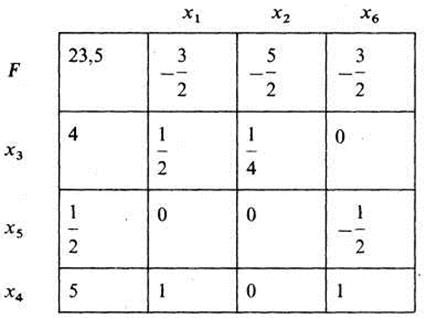
3. Внести коэффициенты при неизвестных в уравнениях и целевой функции в верхней ячейке клеток матрицы 38.2.
4. Выбрать генеральный элемент.
Для этого:
найти в верхней строке матрицы какой-либо положительный элемент (3/2). Если в верхней строке нет положительных элементов, то записанное в данной матрице базисное решение будет оптимальным, т.е. уменьшить значение целевой функции при переходе от одного допустимого базисного решения к другому не представляется возможным;
составить отношение свободных членов (первый столбец матрицы 38.2)
к положительным коэффициентам выбранного
столбца. В рассматриваемом примере
имеют место отношения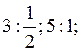 
выбрать среди найденных отношений наименьшее (в примере 5). Если наименьшее отношение достигается при нескольких значениях, то можно выбрать любое. Элемент выбранного столбца, которому соответствует наименьшее отношение, – генеральный элемент (выделен в матрицах).
5. Найти значение, обратное генеральному элементу, внести его в правый угол клетки, содержащий генеральный элемент (в примере 1).
6. Все коэффициенты из верхних отделений строки, где расположен генеральный элемент, умножить на значение, обратное генеральному элементу, и поместить полученные произведения в соответствующие правые углы клеток той же строки.
7. Умножить на значение, обратное генеральному элементу, со знаком «–» все коэффициенты (кроме генерального) из левых углов клеток столбца, где расположен генеральный элемент, и поместить полученные произведения в соответствующие правые углы клеток этого же столбца.
8. Выделить каким-либо способом числа, находящиеся в левых углах клеток строки, где расположен генеральный элемент, и в правых углах клеток столбца, в котором содержится генеральный элемент.
9. Заполнить оставшиеся правые углы клеток числами, полученными перемножением соответствующих выделенных чисел.
10. Перейти к новому набору свободных элементов. Для этого из правых углов клеток строки и столбца, на пересечении которых находится генеральный элемент, перенести все числа в левые углы соответствующей строки и столбца следующей матрицы (для первой итерации матрица 38.3), в левые углы остальных клеток следующей матрицы записать числа, равные алгебраической сумме чисел левого и правого углов соответствующей клетки предыдущей матрицы.
11.Выполнить п. 4.
В верхней строке матрицы все коэффициенты при свободных неизвестных отрицательны, следовательно записанный в данной матрице план формирования обеспечивает оптимальное решение. Таким образом, для освоения расчетных пассажиропотоков требуется ввести в обращение четыре поезда сообщения 1–2, один поезд через день сообщения 2–3 и пять поездов сообщения 3–4. При этом целевая функция достигнет 23,5 стоимостных единиц.
В оперативных условиях может потребоваться решение, при котором неизвестные могут принимать только целочисленные значения. Тогда задача может быть решена с использованием метода отсечения для
целочисленных задач линейного программирования.
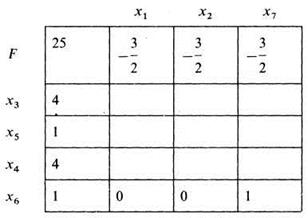
Из матрицы 38.3
.
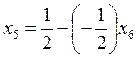Перепишем уравнение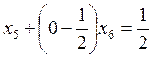 
.
Дробная часть должна быть всегда положительна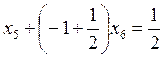 
Следовательно,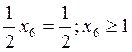 
.
Введя новую переменную, получим х6 = 1 + х7. Введя искусственную переменную, получим Z= 1 – (х6 – х7). Решая новую задачу линейного программирования, учитывающую дополнительное равенство, получим матрицы 38.4 и 38.5.
Таким образом, для освоения пассажиропотока необходимо ввести четыре поезда сообщения 1–2, один поезд сообщения 3–2 и четыре поезда сообщения 2–4.
Наибольшее число назначений определяют исходя из условия
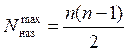, где n – число станций в пределах рассматриваемого полигона, на которых можно сформировать или
обернуть состав пассажирского поезда.
Матрица 38.4
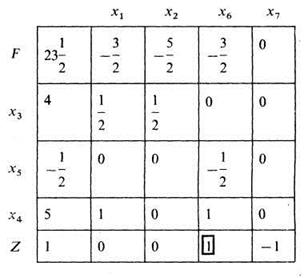
Матрица 38.5
Условие определяет число назначений исходя из того, что каждая станция может быть связана с другой станцией поездом прямого сообщения и не учитывает различных маршрутов следования поездов между ними.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.